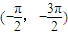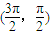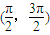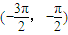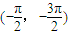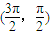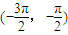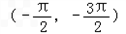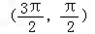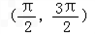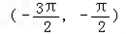Question

已知直线m：x+2y-3=0，函数y=3x+cosx的图象与直线l相切于P点，若l⊥m，则P点的坐标可能是（　　）

Answer 1

分析：先设切点坐标为（m，n），然后得到两个等式f（m）=n，f'（m）=2，利用f'（m）=2得出sinm=1，排除一些选项，最后根据f（m）=n再排除一些选项即可．

解答：解：直线m：x+2y-3=0斜率为-

1

2

，若l⊥m，
则直线l的斜率为2，
∵函数y=3x+cosx的图象与直线l相切于P点，
∴设切点坐标为（m，n）
则n=3m+cosm，且f'（m）=3-sinm=2
∴sinm=1，⇒cosm=0，
∴n=3m，
从而排除A，B，D．
故选C．

点评：本题主要考查了利用导数研究曲线上某点切线方程，以及直线的一般式方程与直线的垂直关系，属于中档题．