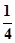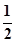题目内容
若实数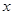
，
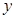满足条件
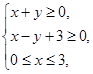则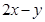
的最大值为___________。
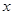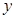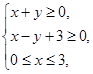，满足条件则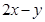的最大值为___________。9
试题分析：画出线性约束条件
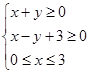的可行域，由此可求目标函数
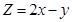的最大值为9.点评：对于解决线性规划的问题我们的关键点在于分析目标函数。目标函数除了我们常见的
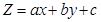这种形式外，还有常见的两种：
，
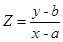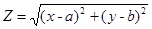第一种的几何意义为：过点
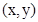与点(a,b)直线的斜率。第二种的几何意义为：点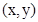与点(a,b)的距离。
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
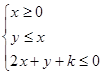（k为常数），若z=x+3y的最大值为8，则k=______________
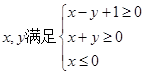，则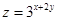
的最大值是（ ）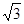
，
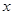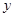满足条件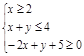
，则目标函数
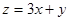的最大值为（ ）
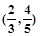是该目标函数z＝ax－y的最优解，则a的取值范围是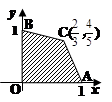
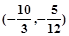
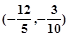
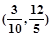
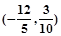
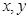满足
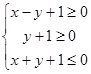，则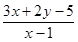
的取值范围是___________
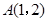，若点
满足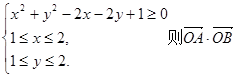
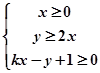表示的平面区域是一个直角三角形，则该直角三角形的面积是（ ）
