题目内容
先阅读下列不等式的证法:
已知a1,a2∈R,a12+a22=1,求证:|a1+a2|≤
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+1,因为对一切x∈R,恒有f(x)≥0,所以△=4(a1+a2)2-8≤0,故得|a1+a2|≤
.
再解决下列问题:
(1)若a1,a2,a3∈R,a12+a22+a32=1,求证|a1+a2+a3|≤
;
(2)试将上述命题推广到n个实数,并证明你的结论.
已知a1,a2∈R,a12+a22=1,求证:|a1+a2|≤
| 2 |
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+1,因为对一切x∈R,恒有f(x)≥0,所以△=4(a1+a2)2-8≤0,故得|a1+a2|≤
| 2 |
再解决下列问题:
(1)若a1,a2,a3∈R,a12+a22+a32=1,求证|a1+a2+a3|≤
| 3 |
(2)试将上述命题推广到n个实数,并证明你的结论.
(1)证明:构造函数f(x)=(x-a1)2+(x-a2)2+(x-a3)2(2分)
则f(x)=3x2-2(a1+a2+a3)x+a12+a22+a32=3x2-2(a1+a2+a3)x+1(2分)
因为对一切x∈R,恒有f(x)≥0,所以△=4(a1+a2+a3)2-12≤0,
故得|a1+a2+a3|≤
. (2分)
(2)推广:若a1,a2,…,an∈R,a12+a22+…+an2=1,则|a1+a2+…+an|≤
. (2分)
证明:构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2,
则f(x)=nx2-2(a1+a2+…+an)x+a12+a22+…+an2=nx2-2(a1+a2+…+an)x+1.
因为对一切x∈R,恒有f(x)≥0,所以△=4(a1+a2+…+an)2-4n≤0,
故得|a1+a2+…+an|≤
. (2分)
则f(x)=3x2-2(a1+a2+a3)x+a12+a22+a32=3x2-2(a1+a2+a3)x+1(2分)
因为对一切x∈R,恒有f(x)≥0,所以△=4(a1+a2+a3)2-12≤0,
故得|a1+a2+a3|≤
| 3 |
(2)推广:若a1,a2,…,an∈R,a12+a22+…+an2=1,则|a1+a2+…+an|≤
| n |
证明:构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2,
则f(x)=nx2-2(a1+a2+…+an)x+a12+a22+…+an2=nx2-2(a1+a2+…+an)x+1.
因为对一切x∈R,恒有f(x)≥0,所以△=4(a1+a2+…+an)2-4n≤0,
故得|a1+a2+…+an|≤
| n |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
先阅读下列不等式的证法,再解决后面的问题:已知![]() ,
,![]() ,求证
,求证![]() .
.
证明:构造函数![]() ,
,![]()
因为对一切![]() ,恒有
,恒有![]() ≥0,所以
≥0,所以![]() ≤0,从而得
≤0,从而得![]() ,
,
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
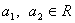 ,
, ,求证
,求证 .
.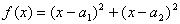 ,
,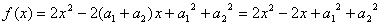
 ,恒有
,恒有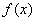 ≥0,所以
≥0,所以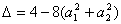 ≤0,从而得
≤0,从而得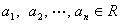 ,
,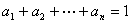 ,请写出上述结论的推广式;
,请写出上述结论的推广式;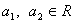 ,
,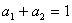 ,求证
,求证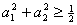 .
.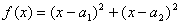 ,
,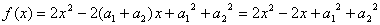
 ,恒有
,恒有 ≥0,所以
≥0,所以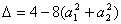 ≤0,从而得
≤0,从而得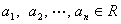 ,
,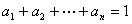 ,请写出上述结论的推广式;
,请写出上述结论的推广式;