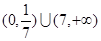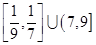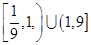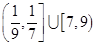题目内容
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为 立方米,且
立方米,且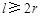 . 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )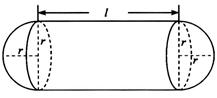
A. | B.1 | C.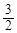 | D.2 |
B
解析试题分析:设容器的容积为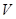 ,由题意知:
,由题意知: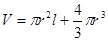 ,又
,又  ,故
,故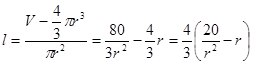 由于
由于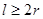 ,因此
,因此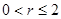 .所以建造费用
.所以建造费用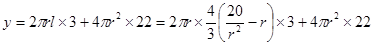 ,因此,
,因此,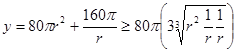 ,此时易知
,此时易知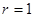 ,故选B.
,故选B.
考点:1.几何体的体积;2.基本不等式.

练习册系列答案
相关题目
定义在R上函数y=f(x)是减函数,且函数y=f(x-1)的图像关于(1,0)成中心对称,若s,t满足不等式f(s2-2s)≤-f(2t-t2),则当1≤s≤4时, 的取值范围是( )
的取值范围是( )
A.  | B. | C.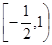 | D. |
已知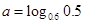 ,
,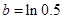 ,
,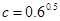 .则( )
.则( )
A.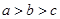 | B.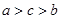 | C.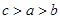 | D.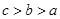 |
已知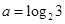 ,
,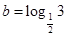 ,
,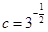 ,则
,则
A.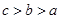 | B.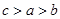 | C.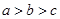 | D.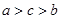 |
指数函数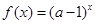 在R上是增函数,则
在R上是增函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.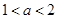 |
如果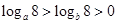 ,那么a、b间的关系是()
,那么a、b间的关系是()
A. | B.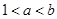 | C.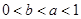 | D.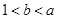 |
已知 ( )
( )
A.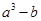 | B.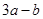 | C.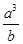 | D.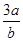 |
若点(a,b)在y=lgx图象上,a≠1,则下列点也在此图象上的是( )
A.(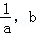 ) ) | B.(10a,1﹣b) |
C.(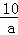 ,b+1) ,b+1) | D.(a2,2b) |
 对任意的x满足
对任意的x满足 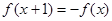 ,当-l≤x<l时,
,当-l≤x<l时, 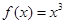 .函数
.函数 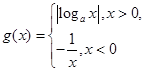 若函数在
若函数在 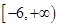 上有6个零点,则实数a的取值范围是( )
上有6个零点,则实数a的取值范围是( )