题目内容
设x,y,z∈R且x+2y+3z=1
(I)当z=1,|x+y|+|y+1|>2时,求x的取值范围;
(II)当x>0,y>0,z>0时,求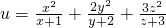 的最小值.
的最小值.
解:(I)当z=1时,∵x+2y+3z=1,∴x+2y=-2,即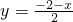
∴|x+y|+|y+1|>2可化简|x-2|+|x|>4,
∴x<0时,-x+2-x>4,∴x<-1;
0≤x≤2时,-x+2+x>4不成立;
x>2时,x-2+x>4,∴x>3
综上知,x<-1或x>3;
(II)∵(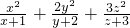 )[(x+1)+2(y+2)+3(z+3)]≥(x+2y+3z)2
)[(x+1)+2(y+2)+3(z+3)]≥(x+2y+3z)2
∴(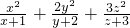 )(x+2y+3z+14)≥(x+2y+3z)2,
)(x+2y+3z+14)≥(x+2y+3z)2,
∴
∴u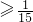 ,当且仅当
,当且仅当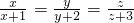 ,又x+2y+3z=1,即x=
,又x+2y+3z=1,即x=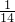 ,y=
,y= ,z=
,z=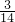 时,umin=
时,umin= .
.
分析:(I)利用条件化二元为一元,再解不等式,即可求x的取值范围;
(II)利用柯西不等式,即可求得u的最小值.
点评:本题考查解不等式,考查函数的最值,正确运用柯西不等式是关键.
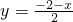
∴|x+y|+|y+1|>2可化简|x-2|+|x|>4,
∴x<0时,-x+2-x>4,∴x<-1;
0≤x≤2时,-x+2+x>4不成立;
x>2时,x-2+x>4,∴x>3
综上知,x<-1或x>3;
(II)∵(
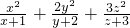 )[(x+1)+2(y+2)+3(z+3)]≥(x+2y+3z)2
)[(x+1)+2(y+2)+3(z+3)]≥(x+2y+3z)2∴(
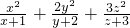 )(x+2y+3z+14)≥(x+2y+3z)2,
)(x+2y+3z+14)≥(x+2y+3z)2,∴

∴u
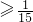 ,当且仅当
,当且仅当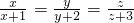 ,又x+2y+3z=1,即x=
,又x+2y+3z=1,即x=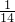 ,y=
,y= ,z=
,z=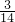 时,umin=
时,umin= .
.分析:(I)利用条件化二元为一元,再解不等式,即可求x的取值范围;
(II)利用柯西不等式,即可求得u的最小值.
点评:本题考查解不等式,考查函数的最值,正确运用柯西不等式是关键.

练习册系列答案
相关题目
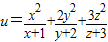 的最小值.
的最小值.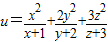 的最小值.
的最小值.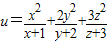 的最小值.
的最小值.