题目内容
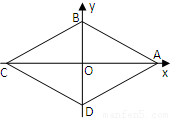
已知菱形ABCD四个顶点对应的复数分别为4,2i,-4,-2i.(1)复数z=x+yi(x,y∈R)满足|z|≤6,求复数z对应的点Z落在菱形ABCD内部的概率;
(2)复数z=x+yi(x,y∈Z)满足|x|≤4,|y|≤2.求复数z对应的点Z落在菱形ABCD外部的概率.
【答案】分析:(1)由于满足|z|≤6所有的点Z的集合是一个圆面,菱形ABCD在其内部,分别求出其面积,利用几何概型的概率计算公式即可得出.
(2)先求出满足条件的所有整点的个数,再求出在菱形外部的整点的个数,利用古典概型的概率计算公式就看得出.
解答:解:(1)满足|z|≤6所有的点Z的集合是一个圆面,其面积是36π.
菱形ABCD在其内部,且面积为16.
故复数z对应的点Z落在菱形内的概率为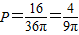 .
.
(2)当复数z的实部与虚部x,y都是整数,且|x|≤4,|y|≤2时,
对应点Z共有9×5=45个.
当x>0,y>0时,共有6个点在菱形ABCD外.由对称性知,共有4×6=24个点在菱形外,
故复数z对应的点Z落在菱形外的概率是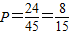 .
.
点评:熟练掌握几何概型的概率、古典概型的概率计算公式、及正确得出基本事件的总数和要求事件所包含基本事件的个数是解题的关键.
(2)先求出满足条件的所有整点的个数,再求出在菱形外部的整点的个数,利用古典概型的概率计算公式就看得出.
解答:解:(1)满足|z|≤6所有的点Z的集合是一个圆面,其面积是36π.
菱形ABCD在其内部,且面积为16.
故复数z对应的点Z落在菱形内的概率为
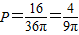 .
.(2)当复数z的实部与虚部x,y都是整数,且|x|≤4,|y|≤2时,
对应点Z共有9×5=45个.
当x>0,y>0时,共有6个点在菱形ABCD外.由对称性知,共有4×6=24个点在菱形外,
故复数z对应的点Z落在菱形外的概率是
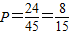 .
.点评:熟练掌握几何概型的概率、古典概型的概率计算公式、及正确得出基本事件的总数和要求事件所包含基本事件的个数是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
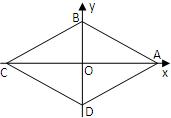 已知菱形ABCD四个顶点对应的复数分别为4,2i,-4,-2i.
已知菱形ABCD四个顶点对应的复数分别为4,2i,-4,-2i.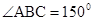 ,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( )
,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率( ) B.
B.
 C.
C.
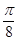 D.
D.
 ;②AB与平面BCD成60°的角;
;②AB与平面BCD成60°的角;