题目内容
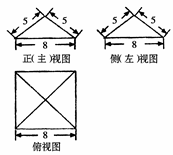
一几何体的主视图,左视图与俯视图如图所示,则该几何体的体积等于( )
| A.2 | B. | C. | D.1 |

C
解析考点:由三视图求面积、体积.
专题:计算题.
分析:几何体是一个不完整的圆柱,首先用和它一样的不完整图形对起来,得到一个完整的圆柱,圆柱的底面直径是2,圆柱的高是4,做出圆柱的体积,得到不完整图形的体积.
解答:解:由三视图知,几何体是一个不完整的圆柱,
首先把几何体补成完整的圆柱,用和它一样的不完整图形对起来,
得到一个完整的圆柱,
圆柱的底面直径是2,圆柱的高是4
∴圆柱的体积是4π×12×4=4π
∴不完整圆柱的体积是 ×4π=2π
×4π=2π
故选C.
点评:本题考查由三视图求体积,考查由三视图还原直观图,考查利用补全的思想来把不能解决的问题转化为我们熟悉的图形,本题是一个基础题.

练习册系列答案
相关题目
在四面体S—ABC中, ,二面角S—AC—B的余弦值是
,二面角S—AC—B的余弦值是 ,则该四面体外接球的表面积是 ( )
,则该四面体外接球的表面积是 ( )
A. | B. | C.24 | D.6 |
两个球体积之和为12π,且这两个球的球大圆周长之和 为6π,那么这两球半径之差是
为6π,那么这两球半径之差是
A. | B.1 | C.2 | D.3 |

 中,
中, 和
和 是全等的正三角形,
是全等的正三角形,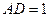 ,则此三棱锥的体积为( )
,则此三棱锥的体积为( ) ,那么正方体的棱长等于 ( )
,那么正方体的棱长等于 ( ) B
B  C
C 
 D
D 
 和
和 ,腰长为
,腰长为 的等腰梯形,则该几何体的体积是 ( )
的等腰梯形,则该几何体的体积是 ( )