题目内容
设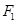 、
、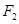 分别为双曲线
分别为双曲线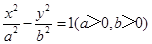 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点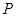 ,满足
,满足 ,且点
,且点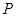 的横坐标为
的横坐标为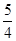
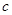 (
(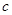 为半焦距),则该双曲线的离心率为( )
为半焦距),则该双曲线的离心率为( )
A.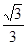 | B. | C.2 | D.2 |
C
解析考点:双曲线的简单性质.
专题:计算题.
解答:解:由题意,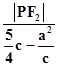 =
=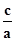
∵|PF2|=|F1F2|,
∴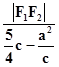 =
=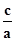
∴ =
=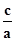
∴5e2-8e-4=0
∴(e-2)(5e+2)=0
∵e>1
∴e=2
故选C.
点评:本题以双曲线为载体,考查双曲线的几何性质,解题的关键是得出几何量之间的关系.

练习册系列答案
相关题目
双曲线 的离心率
的离心率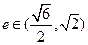 ,则m的取值范围是
,则m的取值范围是
A.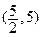 | B.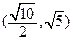  | C.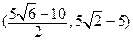 | D.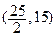 |
已知双曲线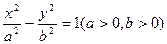 的实轴长、虚轴长、焦距长成等差数列,
的实轴长、虚轴长、焦距长成等差数列,
则此双曲线的离心率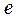 为( )
为( )
| A. | B. | C.2 | D.3 |
若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )
A.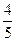 | B.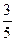 | C.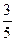 | D.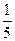 |
双曲线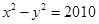 的左、右顶点分别为
的左、右顶点分别为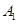 、
、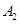 ,P为其右支上的一点,且
,P为其右支上的一点,且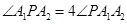 ,则
,则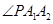 等于( )
等于( )
| A.无法确定 | B.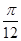 | C.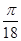 | D.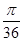 |
设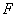 为抛物线
为抛物线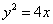 的焦点,
的焦点,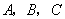 为该抛物线上三点,若
为该抛物线上三点,若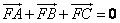 ,则
,则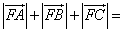
| A.9 | B.6 | C.4 | D.3 |
 轴上的双曲线的右焦点,与双曲线的两个交点分别在左、右两只上,则双曲线的离心率的取值范围是 ( )
轴上的双曲线的右焦点,与双曲线的两个交点分别在左、右两只上,则双曲线的离心率的取值范围是 ( )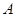

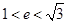
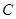
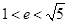
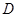
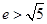
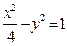
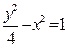
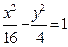

 上的两点,并且满足OA⊥OB.
上的两点,并且满足OA⊥OB.