题目内容
设f(x)=
x3+
ax2+2bx+c，当x∈（0，1）时取得极大值，当x∈（1，2）时取得极小值，则
的取值范围为
| 1 |
| 3 |
| 1 |
| 2 |
| b-3 |
| a+2 |
（-∞，-3）∪（2，+∞）
（-∞，-3）∪（2，+∞）
．分析：据极大值点左边导数为正右边导数为负，极小值点左边导数为负右边导数为正得a，b的约束条件，据线性规划求出最值．
解答：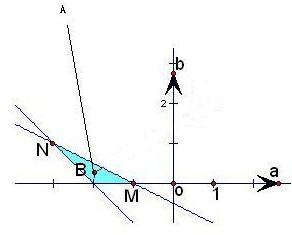
解：∵f(x)=
x3+
ax2+2bx+c，
∴f′（x）=x2+ax+2b，
∵函数f（x）在区间（0，1]内取得极大值，在区间（1，2]内取得极小值
∴f′（x）=x2+ax+2b=0在（0，1]和（1，2]内各有一个根，
f′（0）＞0，f′（1）≤0，f′（2）≥0
即
，
在aOb坐标系中画出其表示的区域，如图，
表示点A（-2，3）与可行域内的点B连线的斜率，
∵M（-1，0），∴kAM=-3，
∵N（-3，1），∴kAN=2，
结合图象知
的取值范围是（-∞，-3）∪（2，+∞）．
故答案为：（-∞，-3）∪（2，+∞）．
解：∵f(x)=| 1 |
| 3 |
| 1 |
| 2 |
∴f′（x）=x2+ax+2b，
∵函数f（x）在区间（0，1]内取得极大值，在区间（1，2]内取得极小值
∴f′（x）=x2+ax+2b=0在（0，1]和（1，2]内各有一个根，
f′（0）＞0，f′（1）≤0，f′（2）≥0
即
|
在aOb坐标系中画出其表示的区域，如图，
| b-3 |
| a+2 |
∵M（-1，0），∴kAM=-3，
∵N（-3，1），∴kAN=2，
结合图象知
| b-3 |
| a+2 |
故答案为：（-∞，-3）∪（2，+∞）．
点评：本题考查学生利用导数研究函数极值的能力，综合性强，难度大，对数学思维能力要求较高，要求学生会进行简单的线性规划的能力．
练习册系列答案
相关题目