Question

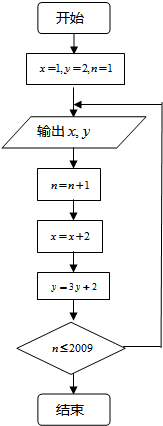30、根据如图所示的程序框图，将输出的x，y值依次分别记为x₁，x₂，…x_n，…，x₂₀₀₉；y₁，y₂，…，y_n，…，y₂₀₀₉．
（1）求数列{x_n}的通项公式x_n；
（2）写出y₁，y₂，y₃，y₄，由此猜想出数列{y_n}的一个通项公式；
（3）求Z_n=x₁y₁+x₂y₂+…+x_ny_n（x∈N^*，n≤2009）．

Answer 1

分析：（1）由框图，知数列x_n中，x₁=1，x_n+1=x_n+2，由此能导出x_n．
（2）y₁=2，y₂=8，y₃=26，y₄=80．由此，猜想y_n=3ⁿ-1（n∈N^*，n≤2008）．然后构造成等比数列进行证明．
（3）z_n=x₁y₁+x₂y₂++x_ny_n=1×（3-1）+3×（3²-1）+5×（3³-1）++（2n-1）×（3ⁿ-1）=1×3+3×3²+5×3³++（2n-1）×3ⁿ-（1+3+5++2n-1）然后用错位相减法进行求解．

解答：解：（1）由程序框图可知：{x_n}是等差数列，且首项x₁=1，公差d=2
∴x_n=1+2（n-1）=2n-1…（3分）
（2）y₁=2=3-1，y₂=3×2+2=8=3²-1，y₃=3×8+2=26=3³-1y₄=3×26+2=80=3⁴-1
故y_n=3ⁿ-1…（7分）
（3）x_n•y_n=（2n-1）（3ⁿ-1）=（2n-1）•3ⁿ-（2n-1）z_n
=（3-1）+（3•3²-3）+（5•3³-5）+…+[（2n-1）•3ⁿ-（2n-1）]
=3+3•3²+5•3³+…+（2n-1）•3ⁿ-[1+3+5+（2n-1）]
=3+3•3²+5•3³+…+（2n-1）•3ⁿ-n²
令S_n=3+3•3²+5•3³+…+（2n-1）•3ⁿ3S_n
=3²+3•3³+5•3⁴+…+（2n-1）•3ⁿ⁺¹
∴-2S_n=3+2（3²+3³+3⁴+…+3ⁿ）-（2n-1）•3ⁿ⁺¹
=2（1-n）•3ⁿ⁺¹-6
∴S_n=（n-1）•3ⁿ⁺¹+3
∴z_n=（n-1）•3ⁿ⁺¹+3-n²…（14分）

点评：本题考查数列的性质和应用，解题时要认真审题，仔细求解，注意错位相减法和构造成法的灵活运用．