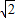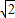题目内容
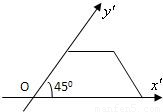
 一梯形的直观图是一个如图所示的等腰梯形,且梯形OA′B′C′的面积为
一梯形的直观图是一个如图所示的等腰梯形,且梯形OA′B′C′的面积为| 2 |
4
4
.分析:根据斜二测画法的规则将图形还原,平面图是一个直角梯形,易求原梯形的面积.
解答:解:如图:
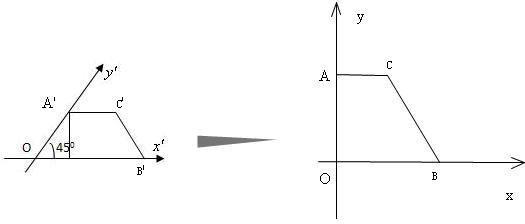
由斜二测画法原理知,平面中的图形与直观图中的图形上下底边的长度是一样的,不一样的是两个梯形的高,
其高的关系是这样的:
平面图中的高OA是直观图中OA'长度的2倍,如直观图,
OA'的长度是直观图中梯形的高的
倍,
由此平面图中梯形的高OA的长度是直观图中梯形高的2×
=2
倍,
故其面积是梯形OA′B′C′的面积2
倍,梯形OA′B′C′的面积为
,
所以原梯形的面积是4.
故答案为:4.

由斜二测画法原理知,平面中的图形与直观图中的图形上下底边的长度是一样的,不一样的是两个梯形的高,
其高的关系是这样的:
平面图中的高OA是直观图中OA'长度的2倍,如直观图,
OA'的长度是直观图中梯形的高的
| 2 |
由此平面图中梯形的高OA的长度是直观图中梯形高的2×
| 2 |
| 2 |
故其面积是梯形OA′B′C′的面积2
| 2 |
| 2 |
所以原梯形的面积是4.
故答案为:4.
点评:本题考查斜二测画法作图规则,掌握斜二测画法的法则是解决问题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
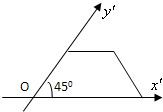 一梯形的直观图是一个如图所示的等腰梯形,且梯形OA′B′C′的面积为
一梯形的直观图是一个如图所示的等腰梯形,且梯形OA′B′C′的面积为| 2 |
| A、2 | ||
B、
| ||
C、2
| ||
| D、4 |
 ,则原梯形的面积为(
)
,则原梯形的面积为(
)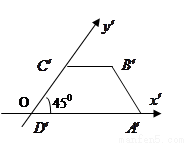
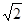 ,则原梯形的面积为( )
,则原梯形的面积为( ) 
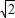 ,则原梯形的面积为( )
,则原梯形的面积为( )