题目内容
以平行六面体ABCD-A1B1C1D1的任意三个顶点为顶点作三角形,从中随机取出2个三角形,则这2个三角形不共面的概率P为( )A.
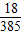
B.
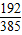
C.
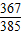
D.
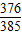
【答案】分析:根据平行六面体的几何特征,我们可以求出以平行六面体ABCD-A1B1C1D1的任意三个顶点为顶点作三角形的总个数,及从中随机取出2个三角形的情况总数,再求出这两个三角形共面的情况数,即可得到这两个三角形不共面的情况数,代入古典概型概率公式,即可得到答案.
解答:解:∵平行六面体ABCD-A1B1C1D1的8个顶点任意三个均不共线
故从8个顶点中任取三个均可构成一个三角形共有C83=56个三角形,从中任选两个,共有C562=1540种情况
从8个顶点中4点共面共有12种情况(六个面,六个对角面),每个面的四个顶点共确定6个不同的三角形
故任取出2个三角形,则这2个三角形不共面共有1540-12×6=1468种
故从中随机取出2个三角形,则这2个三角形不共面的概率P= =
=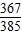
故选C
点评:本题考查的知识点是等可能事件的概率,古典概型概率计算公式,棱柱的结构特征,其中根据棱柱的结构特征,求出基本事件总个数和满足条件的基本事件个数是解答本题的关键.
解答:解:∵平行六面体ABCD-A1B1C1D1的8个顶点任意三个均不共线
故从8个顶点中任取三个均可构成一个三角形共有C83=56个三角形,从中任选两个,共有C562=1540种情况
从8个顶点中4点共面共有12种情况(六个面,六个对角面),每个面的四个顶点共确定6个不同的三角形
故任取出2个三角形,则这2个三角形不共面共有1540-12×6=1468种
故从中随机取出2个三角形,则这2个三角形不共面的概率P=
 =
=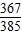
故选C
点评:本题考查的知识点是等可能事件的概率,古典概型概率计算公式,棱柱的结构特征,其中根据棱柱的结构特征,求出基本事件总个数和满足条件的基本事件个数是解答本题的关键.

练习册系列答案
相关题目
以平行六面体ABCD-A1B1C1D1的任意三个顶点为顶点作三角形,从中随机取出2个三角形,则这2个三角形不共面的概率P为( )
A、
| ||
B、
| ||
C、
| ||
D、
|