题目内容
(06年安徽卷)(12分)
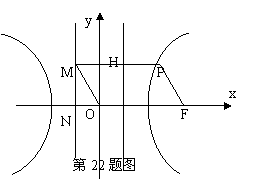
如图,P是边长为1的正六边形ABCDEF所在平面外一点,![]() ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明![]() ⊥
⊥![]() ;
;
(Ⅱ)求面![]() 与面
与面![]() 所成二面角的大小。
所成二面角的大小。

解析:(Ⅰ)在正六边形ABCDEF中,![]() 为等腰三角形,
为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形,∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;又∵正六边形ABCDEF的边长为1,∴![]() ,
,![]() ,
,![]() 。
。
过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,所以![]() 为所求二面角平面角。
为所求二面角平面角。
在![]() 中,OH=
中,OH=![]() ,
,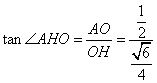 =
=![]() 。
。
在![]() 中,
中,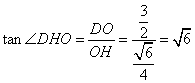 ;
;
而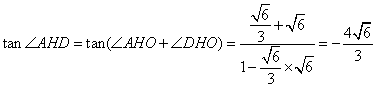
(Ⅱ)以O为坐标原点,建立空间直角坐标系,P(0,0,1),A(0,![]() ,0),B(
,0),B(![]() ,0,0),D(0,2,0),∴
,0,0),D(0,2,0),∴![]() ,
,![]() ,
,![]()
设平面PAB的法向量为![]() ,则
,则![]() ,
,![]() ,得
,得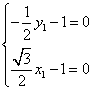 ,
,![]() ;
;
设平面PDB的法向量为![]() ,则
,则![]() ,
,![]() ,得
,得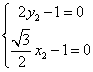 ,
,![]() ;
;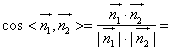

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目