题目内容
椭圆两焦点为 F1(-4,0),F2(4,0),P在椭圆上,若△PF1F2的面积的最大值为12,则该椭圆的标准方程为
- A.
 +
+ =1
=1 - B.
 +
+ =1
=1 - C.
 +
+ =1
=1 - D.
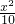 +
+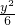 =1
=1
A
分析:由椭圆图象可知,当△PF1F2的面积的最大值为12,P与短轴顶点重合,根据三角形面积公式可得,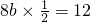 ,所以b=3,由此能够推导出该椭圆的标准方程.
,所以b=3,由此能够推导出该椭圆的标准方程.
解答:由椭圆图象可知,
当△PF1F2的面积的最大值为12,P与短轴顶点重合.
根据三角形面积公式,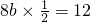 ,所以 b=3,
,所以 b=3,
由 a2=b2+c2得,a=5,
∴椭圆的标准方程为 .
.
故选A.
点评:本题考查椭圆的性质和应用,解题时要注意合理地选用公式.
分析:由椭圆图象可知,当△PF1F2的面积的最大值为12,P与短轴顶点重合,根据三角形面积公式可得,
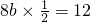 ,所以b=3,由此能够推导出该椭圆的标准方程.
,所以b=3,由此能够推导出该椭圆的标准方程.解答:由椭圆图象可知,
当△PF1F2的面积的最大值为12,P与短轴顶点重合.
根据三角形面积公式,
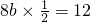 ,所以 b=3,
,所以 b=3,由 a2=b2+c2得,a=5,
∴椭圆的标准方程为
 .
.故选A.
点评:本题考查椭圆的性质和应用,解题时要注意合理地选用公式.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目