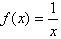题目内容
在下列4个函数:①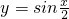 ;②y=sinx;③y=-tanx;④y=-cos2x、其中在区间
;②y=sinx;③y=-tanx;④y=-cos2x、其中在区间 上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上)________.
上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上)________.
④
分析:根据正弦函数的最小正周期T= 求得①②中函数的最小正周期,可判断其正误;结合正弦函数的单调性可判断③;根据余弦函数的最小正周期和单调性可判断④.
求得①②中函数的最小正周期,可判断其正误;结合正弦函数的单调性可判断③;根据余弦函数的最小正周期和单调性可判断④.
解答:y=sin 的最小正周期T=
的最小正周期T=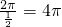 ,不符合要求;
,不符合要求;
y=sinx的最小正周期T=2π,不符合题意;
y=-tanx的最小正周期T=π但是在 上单调递减,不符合题意;
上单调递减,不符合题意;
y=-cos2x的最小正周期T= ,令2kπ≤2x≤π+2kπ,∴kπ≤x≤
,令2kπ≤2x≤π+2kπ,∴kπ≤x≤
∴y=-cos2x在[kπ, ]上单调递增,故在区间
]上单调递增,故在区间 上增,满足条件.
上增,满足条件.
故答案为:④
点评:本题主要考查正弦函数、正切函数和余弦函数的最小正周期的求法和单调性.考查三角函数的基本性质的应用.
分析:根据正弦函数的最小正周期T=
 求得①②中函数的最小正周期,可判断其正误;结合正弦函数的单调性可判断③;根据余弦函数的最小正周期和单调性可判断④.
求得①②中函数的最小正周期,可判断其正误;结合正弦函数的单调性可判断③;根据余弦函数的最小正周期和单调性可判断④.解答:y=sin
 的最小正周期T=
的最小正周期T=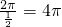 ,不符合要求;
,不符合要求;y=sinx的最小正周期T=2π,不符合题意;
y=-tanx的最小正周期T=π但是在
 上单调递减,不符合题意;
上单调递减,不符合题意;y=-cos2x的最小正周期T=
 ,令2kπ≤2x≤π+2kπ,∴kπ≤x≤
,令2kπ≤2x≤π+2kπ,∴kπ≤x≤
∴y=-cos2x在[kπ,
 ]上单调递增,故在区间
]上单调递增,故在区间 上增,满足条件.
上增,满足条件.故答案为:④
点评:本题主要考查正弦函数、正切函数和余弦函数的最小正周期的求法和单调性.考查三角函数的基本性质的应用.

练习册系列答案
相关题目