题目内容
已知g(x)=ln(ex+b)(b为常数)是实数集R上的奇函数,当g(x)>0时,有f(x)=lng(x)+| a |
| x |
(1)求b的值;
(2)若函数f(x)在[1,e]上的最小值是
| 3 |
| 2 |
分析:(1)利用奇函数的定义进行整理化简是解决本体的关键,注意对数运算性质的灵活运用,指数运算性质的运用和变形,以及恒成立问题的处理方法;
(2)利用导数作为工具求解该函数在闭区间上的最值是解决本题的关键,根据该函数在何处取到最值列出关于a的方程达到求解a的目的.
(2)利用导数作为工具求解该函数在闭区间上的最值是解决本题的关键,根据该函数在何处取到最值列出关于a的方程达到求解a的目的.
解答:解:(1)∵g(-x)=-g(x)∴ln(e-x+b)+ln(ex+b)=0?(e-x+b)(ex+b)=1
?(e-x+ex)b+b2=0?(e-x+ex+b)b=0?b=0.
(2)由(1)知f(x)=lnx+
(x>0),则f′(x)=
-
=
在[1,e]上,讨论如下:
①当a<1时,f'(x)>0,函数f(x)单调递增,其最小值为f(1)=a<1,
这与函数在[1,e]上的最小值是
相矛盾;
②当a=1时,函数f(x)在(1,e]单调递增,其最小值为f(1)=1,同样与最小值是
相矛盾;
③当1<a<e时,函数f(x)在[1,a)上有f'(x)<0,单调递减,
在(a,e]上有f''(x)>0,单调递增,所以函数f(x)满足最小值为f(a)=lna+1
由lna+1=
,得a=
.
④当a=e时,函数f(x)在[1,e)上有f'(x)<0,单调递减,其最小值为f(e)=2,还与最小值是
相矛盾;
⑤当a>e时,显然函数f(x)在[1,e]上单调递减,其最小值为f(e)=1+
>2,
仍与最小值是
相矛盾;综上所述,a的值为
.
?(e-x+ex)b+b2=0?(e-x+ex+b)b=0?b=0.
(2)由(1)知f(x)=lnx+
| a |
| x |
| 1 |
| x |
| a |
| x2 |
| x-a |
| x2 |
在[1,e]上,讨论如下:
①当a<1时,f'(x)>0,函数f(x)单调递增,其最小值为f(1)=a<1,
这与函数在[1,e]上的最小值是
| 3 |
| 2 |
②当a=1时,函数f(x)在(1,e]单调递增,其最小值为f(1)=1,同样与最小值是
| 3 |
| 2 |
③当1<a<e时,函数f(x)在[1,a)上有f'(x)<0,单调递减,
在(a,e]上有f''(x)>0,单调递增,所以函数f(x)满足最小值为f(a)=lna+1
由lna+1=
| 3 |
| 2 |
| e |
④当a=e时,函数f(x)在[1,e)上有f'(x)<0,单调递减,其最小值为f(e)=2,还与最小值是
| 3 |
| 2 |
⑤当a>e时,显然函数f(x)在[1,e]上单调递减,其最小值为f(e)=1+
| a |
| e |
仍与最小值是
| 3 |
| 2 |
| e |
点评:本题考查函数奇偶性的运用,考查学生运用奇偶性定义进行未知数求解的思想和方法.考查函数的导数工具作用,考查学生运用导数解决函数的最值的思想和方法,考查学生运用分类讨论思想和方法解题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
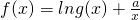 .
. ,求a的值.
,求a的值.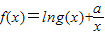 .
. ,求a的值.
,求a的值.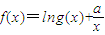 .
. ,求a的值.
,求a的值.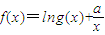 .
. ,求a的值.
,求a的值.