题目内容
设函数f(x)=2x﹣cos4x,{an}是公差为 的等差数列,f(a1)+f(a2)+…+f(a8)=11π,则
的等差数列,f(a1)+f(a2)+…+f(a8)=11π,则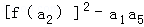 =( )
=( ) 0
0 
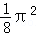
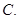
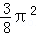
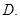
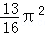
C
解析试题分析:因为 的周期为
的周期为 ,所以
,所以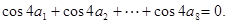 所以
所以 而
而 所以
所以 因此
因此 选C.
选C.
考点:等差数列,三角函数性质

练习册系列答案
相关题目
设等差数列 的前n项和为
的前n项和为 ,若
,若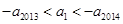 ,则必定有
,则必定有
A.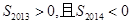 | B.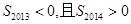 |
C.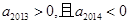 | D. |
已知数列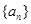 的各项均为正数,执行程序框图(如右图),当
的各项均为正数,执行程序框图(如右图),当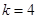 时,
时,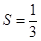 ,则
,则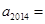 ( )
( )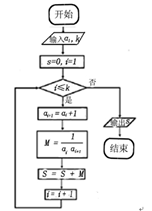
| A.2012 | B.2013 | C.2014 | D.2015 |
若 为等差数列,
为等差数列, 数列
数列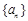 满足
满足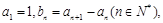 则
则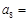 ( )
( )
| A.56 | B.57 | C.72 | D.73 |
下面是关于公差 的等差数列
的等差数列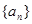 的四个命题:
的四个命题: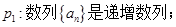
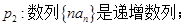
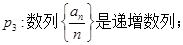
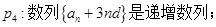
其中的真命题为( )
A.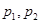 | B.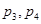 | C.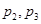 | D.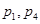 |
已知等比数列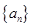 的前
的前 项和为
项和为 ,
, ,且满足
,且满足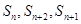 成等差数列,则
成等差数列,则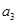 等于( )
等于( )
A. | B. | C.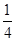 | D. |
等差数列{an}中,S15>0,S16<0,则使an>0成立的n的最大值为( )
| A.6 | B.7 | C.8 | D.9 |
设等差数列{an}的前n项和为Sn,Sm-1=-2,Sm=0,Sm+1=3,则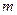 = ( )
= ( )
| A.3 |
| B.4 |
| C.5 |
| D.6 |
等差数列{an}中,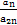 是一个与n无关的常数,则该常数的可能值的集合为( )
是一个与n无关的常数,则该常数的可能值的集合为( )
| A.{1} | B.{1, } } |
C.{ } } | D.{0, ,1} ,1} |