题目内容
（00全国卷文）（本小题满分14分）
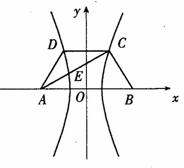
如图，已知梯形ABCD中
，点E分有向线段
所成的比为
，双曲线过C、D、E三点，且以A、B为焦点
求双曲线的离心率
解析：如图，以AB为垂直平分线为
轴，直线AB为
轴，建立直角坐标系
，则CD⊥轴
因为双曲线经过点C、D，且以A、B为焦点，由双曲线的对称性知C、D关于轴对称 ――2分
依题意，记A
，B
，C
，其中
为双曲线的半焦距，
，
是梯形的高
由定比分点坐标公式，得点E的坐标为
，
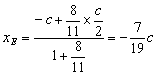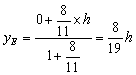
――5分
设双曲线的方程为
，则离心率
由点C、E在双曲线上，得
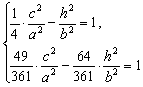――10分
由①得
，代入②得
所以，离心率
――14分
练习册系列答案
相关题目
为等差数列，
为数列
项和，已知
，
，
为数列
的前