题目内容
计算由曲线y=9-x2与直线y=x+7围成的封闭区域的面积为
.
| 9 |
| 2 |
| 9 |
| 2 |
分析:先求出两曲线的交点坐标,根据积分的几何意义即可求封闭区域的面积.
解答:S=∫_-21(9-x2-x-7)解:将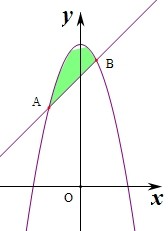 y=x+7代入y=9-x2,
y=x+7代入y=9-x2,
得x+7=9-x2,
即x2+x-2=0,
解得x=1或x=-2,
∴由积分的几何意义可知封闭区域的面积S=
(9-x2-x-7)dx=(-
x3-
x2+2x)|
=(-
-
+2)-(
×8-
×4-2×2)=
.
故答案为:
 y=x+7代入y=9-x2,
y=x+7代入y=9-x2,得x+7=9-x2,
即x2+x-2=0,
解得x=1或x=-2,
∴由积分的几何意义可知封闭区域的面积S=
| ∫ | 1 -2 |
| 1 |
| 3 |
| 1 |
| 2 |
1 -2 |
=(-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题主要考查积分的几何意义,要求熟练掌握常见函数的积分公式.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目