题目内容
将y=sin(2x+
)的图象向右平移
个单位长度后,再使平移后的图象纵坐标不变,横坐标伸长为原来的2倍,得到函数y=f(x)的图象,将方程xf(x)=1的所有正根按从小到大排成一个数列{an},在以下结论中:
①a2k+2-a2k>2π(k∈N*); ②
(an+1-an)=π;
③a2k-1+a2k>(4k-3)π(k∈N*); ④a2k+a2k+1>(4k-1)π(k∈N*)
正确结论的个数有( )
| π |
| 3 |
| π |
| 6 |
①a2k+2-a2k>2π(k∈N*); ②
| lim |
| n→∞ |
③a2k-1+a2k>(4k-3)π(k∈N*); ④a2k+a2k+1>(4k-1)π(k∈N*)
正确结论的个数有( )
| A、1 | B、2 | C、3 | D、4 |
分析:项根据的三角函数的图象变换求出f(x)的解析式,然后将方程xf(x)=1的所有正根转化成y=f(x)与y=
的图象在第一象限的交点横坐标,然后画出两函数的图形,结合图形可判定选项的真假.
| 1 |
| x |
解答:解:将y=sin(2x+
)的图象向右平移
个单位长度后,
得到图象的解析式为y=sin[2(x-
)+
]=sin2x,
再使平移后的图象纵坐标不变,横坐标伸长为原来的2倍,得到y=f(x)=sinx,
方程xf(x)=1的所有正根即为y=f(x)与y=
的图象在第一象限的交点横坐标
画出图形如下图
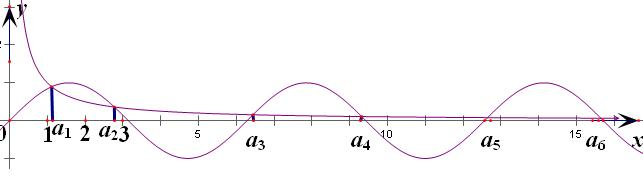
观察图形可知
①a2k+2-a2k>2π(k∈N*)正确; ②
(an+1-an)=π,正确;
③a2k-1+a2k>(4k-3)π(k∈N*)正确; ④a2k+a2k+1>(4k-1)π(k∈N*),当k=1时,不成立
故选C.
| π |
| 3 |
| π |
| 6 |
得到图象的解析式为y=sin[2(x-
| π |
| 6 |
| π |
| 3 |
再使平移后的图象纵坐标不变,横坐标伸长为原来的2倍,得到y=f(x)=sinx,
方程xf(x)=1的所有正根即为y=f(x)与y=
| 1 |
| x |
画出图形如下图

观察图形可知
①a2k+2-a2k>2π(k∈N*)正确; ②
| lim |
| n→∞ |
③a2k-1+a2k>(4k-3)π(k∈N*)正确; ④a2k+a2k+1>(4k-1)π(k∈N*),当k=1时,不成立
故选C.
点评:本题主要考查了函数与方程,以及数列与函数的综合,同时考查了数形结合的思想,属于中档题.

练习册系列答案
相关题目
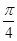 )的图象
)的图象 个单位长度 B.向右平移
个单位长度 B.向右平移