题目内容
已知函数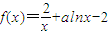
(Ⅰ)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求a的值;
(Ⅱ)若f(x)≥0在x∈[1,+∞)上恒成立,求a的范围.
【答案】分析:(Ⅰ)求导函数,利用曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,建立方程,即可求a的值;
(Ⅱ)求导函数,分类讨论,确定函数的单调性,即可求得a的范围.
解答:解:(Ⅰ)函数y=f(x)的导数为f′(x)=-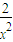 +
+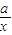 ,则
,则
∵曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,直线y=x+2的斜率为1,
∴f′(1)=-2+a=-1,∴a=1;
(Ⅱ)求导数可得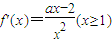
a≥2时,f′(x)≥0,函数在x∈[1,+∞)上单调递增,∴f(x)min=f(1)=0,满足题意;
a<2时,f′(x)<0,函数在x∈[1,+∞)上单调递减,∴f(x)max=f(1)=0,不满足题意
综上,a的范围为[2,+∞).
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,属于中档题.
(Ⅱ)求导函数,分类讨论,确定函数的单调性,即可求得a的范围.
解答:解:(Ⅰ)函数y=f(x)的导数为f′(x)=-
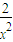 +
+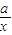 ,则
,则∵曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,直线y=x+2的斜率为1,
∴f′(1)=-2+a=-1,∴a=1;
(Ⅱ)求导数可得
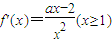
a≥2时,f′(x)≥0,函数在x∈[1,+∞)上单调递增,∴f(x)min=f(1)=0,满足题意;
a<2时,f′(x)<0,函数在x∈[1,+∞)上单调递减,∴f(x)max=f(1)=0,不满足题意
综上,a的范围为[2,+∞).
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,属于中档题.

练习册系列答案
相关题目











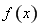


 .
. 在
在 和
和 处的切线相互平行,求
处的切线相互平行,求 的值;
的值; ,对任意的
,对任意的 ,均存在
,均存在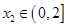 ,使得
,使得 .试求实数
.试求实数 。
。 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值; 在区间(
在区间( ,
,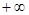 )内是增函数,求
)内是增函数,求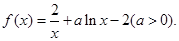
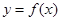 在点
在点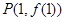 处的切线与直线
处的切线与直线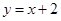 垂直,求函数
垂直,求函数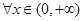 都有
都有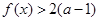 成立,试求实数a的取值范围;
成立,试求实数a的取值范围;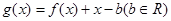 ,当a=1时,函数
,当a=1时,函数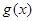 在区间
在区间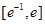 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。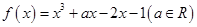
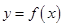 在
在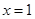 处与直线
处与直线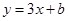 相切,求
相切,求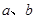 的值;
的值;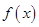 在区间
在区间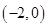 内有极值,求
内有极值,求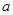 的取值范围.
的取值范围.