题目内容
函数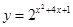 的单调递减区间是 .
的单调递减区间是 .
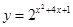 的单调递减区间是 .
的单调递减区间是 .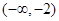
试题分析:因为函数
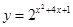 的外层是y=2x,内层是y=
的外层是y=2x,内层是y= ,那么根据复合函数单调性可知,外层是递增函数,内层的递减区间即为所求,那么根据二次函数的性质可知,函数的递减区间为
,那么根据复合函数单调性可知,外层是递增函数,内层的递减区间即为所求,那么根据二次函数的性质可知,函数的递减区间为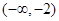 ,故所求的单调递减区间是
,故所求的单调递减区间是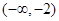 ,答案为
,答案为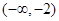 。
。点评:解决该试题的关键是复合函数单调性的原则:同增异减的思想。那么首要的分析定义域,然后分析单调性,内外结合得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
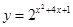 的单调递减区间是 .
的单调递减区间是 .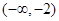
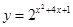 的外层是y=2x,内层是y=
的外层是y=2x,内层是y= ,那么根据复合函数单调性可知,外层是递增函数,内层的递减区间即为所求,那么根据二次函数的性质可知,函数的递减区间为
,那么根据复合函数单调性可知,外层是递增函数,内层的递减区间即为所求,那么根据二次函数的性质可知,函数的递减区间为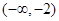 ,故所求的单调递减区间是
,故所求的单调递减区间是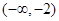 ,答案为
,答案为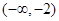 。
。
 阅读快车系列答案
阅读快车系列答案