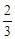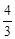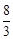题目内容
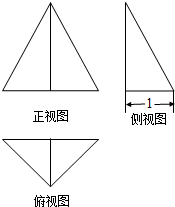
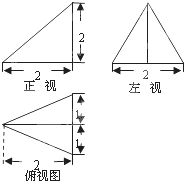 已知某个三棱锥的三视图如图,根据图中标出的尺寸(单位:cm),则这个三棱锥的体积是( )
已知某个三棱锥的三视图如图,根据图中标出的尺寸(单位:cm),则这个三棱锥的体积是( )分析:俯视图是等腰三角形,且内部有一条实线,该实线是三棱锥的一条侧棱在地面上的垂直投影,所以棱锥顶点在底面的射影为底面三角形一边的中点,结合正视和左视图即可还原得到原图形,底面积可求,高已知,则体积可求.
解答:解:由三视图可得原几何体如图,

底面三角形ABC是以BC为底边的等腰三角形,且BD=DC=1,AD=2,
面PBC⊥面ABC,PD=2为棱锥的高,
所以VP-ABC=
×S△ABC×PD=
×
×2×2×2=
cm3.
故选C.

底面三角形ABC是以BC为底边的等腰三角形,且BD=DC=1,AD=2,
面PBC⊥面ABC,PD=2为棱锥的高,
所以VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
故选C.
点评:本题考查了由三视图求几何体的体积,解答的关键是由三视图还原得到原几何体,由三视图得原几何体的方法是,先看俯视图,结合正视图和左视图.此题是基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
 已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于( )
已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
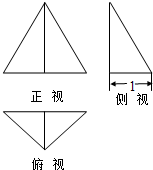 已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形则此三棱锥的体积等于
已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形则此三棱锥的体积等于
 ),则这个三棱锥的体积是
),则这个三棱锥的体积是
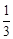
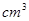 B.
B.