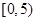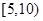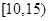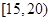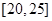题目内容
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
|
组别 |
候车时间 |
人数 |
|
一 |
|
2 |
|
二 |
|
6 |
|
三 |
|
4 |
|
四 |
|
2 |
|
五 |
|
1 |
【答案】
(1)32 ;(2)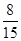 .
.
【解析】
试题分析:(1)利用比例关系求第一问;(2)详细找出所有事件的情况,在所有情况中找到符合题意的情况,再求概率.
试题解析:(1)由频率分布表可知:这15名乘客中候车时间少于10分钟的人数为8,
所以,这60名乘客中候车时间少于10分钟的人数大约等于 人. 4分
人. 4分
(2)设第三组的乘客为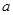 ,
,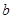 ,
,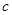 ,
,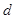 ,,第四组的乘客为1,2;
,,第四组的乘客为1,2;
“抽到的两个人恰好来自不同的组”为事件 . 5分
. 5分
所得基本事件共有15种,即:
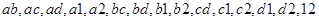 8分
8分
其中事件 包含基本事件,共8种, 10分
包含基本事件,共8种, 10分
由古典概型可得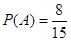 ,
12分.
,
12分.
考点:1.频率分布表;2.概率.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
| 组别 | 候车时间 |
|
|
| [0,5) | 2 |
| 二 | [5,10) | 6 |
| 三 | [10,15) | 4 |
| 四 | [15,20) | 2 |
| 五 | [20,25] | 1 |
(1)求这15名乘客的平![]() 均候车时间.
均候车时间.
(2)估计这6![]() 0名乘客中候车时间少于10分钟的人数.
0名乘客中候车时间少于10分钟的人数.
(3)若从上表第三和第四组的6人中随机抽取2人进行问卷调查,求抽到的两人恰好来自不同组的概率.
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
(Ⅰ)求这15名乘客的平均候车时间;
(Ⅱ)估计这60名乘客中候车时间少于10分钟的人数;
(Ⅲ)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
| 组别 | 候车时间 | 人数 |
| 一 | [0,5) | 2 |
| 二 | [5,10) | 6 |
| 三 | [10,15) | 4 |
| 四 | [15,20) | 2 |
| 五 | [20,25] | 1 |
(Ⅱ)估计这60名乘客中候车时间少于10分钟的人数;
(Ⅲ)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.