题目内容
如右图所示，正方形ABCD，ABEF的边长都是1，并且平面ABCD⊥平面ABEF，点M在AC上移动，点N在BF上移动．若|CM|＝|BN|＝a(0<a<
)．
(1)求MN的长度；
(2)当a为何值时，MN的长度最短？
[解析] 因为平面ABCD⊥平面ABEF，且交线为AB，BE⊥AB，所以BE⊥平面ABCD，所以BA，BC，BE两两垂直．取B为坐标原点，过BA，BE，BC的直线分别为x轴，y轴和z轴，建立如图所示的空间直角坐标系．
因为|BC|＝1，|CM|＝a，点M在坐标平面xBz内且在正方形ABCD的对角线上，所以点
因为点N在坐标平面xBy内且在正方形ABEF的对角线上，|BN|＝a，所以点N(
a，a,0)．
练习册系列答案
相关题目
如右图所示，点P在边长为1的正方形的边上运动，设M是CD边的中点，则当点P沿着A-B-C-M运动时，以点P经过的路程x为自变量，三角形APM的面积函数的图象形状大致是（ ）
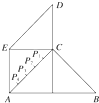某县位于山区，居民的居住区域大致呈如右图所示的五边形，近似由一个正方形和两个等腰直角三角形组成，若AB=60km，AE=CD=30km，为了解决当地人民看电视难的问题，准备建一个电视转播台，理想方案是转播台距五边形各顶点的距离平方和最小，图中P1、P2、P3、P4是AC的五等分点，则转播台应建在（ ）
由两个完全相同的正四棱锥组合而成的空间几何体的正（主）视图、侧（左）视图、俯视图相同如右图所示，其中视图中四边形ABCD是边长为1的正方形，则该几何体的体积为（ ）