题目内容
过抛物线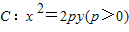 的焦点F作直线l与抛物线C交于A、B两点,当点A的纵坐标为1时,|AF|=2.
的焦点F作直线l与抛物线C交于A、B两点,当点A的纵坐标为1时,|AF|=2.(1)求抛物线C的方程;
(2)若抛物线C上存在一点M,使得MA⊥MB,求直线l的斜率k的取值范围.
【答案】分析:(1)利用抛物线的定义,结合|AF|=2,即可求得抛物线的方程;
(2)直线方程代入抛物线方程,利用韦达定理及MA⊥MB,建立方程,即可求直线l的斜率k的取值范围.
解答:解:(1)∵|AF|=2,∴由抛物线的定义,可得1+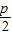 =2,∴p=2
=2,∴p=2
∴抛物线C的方程为x2=4y;
(2)抛物线C的焦点为F(0,1),设直线l的方程为y=kx+1,A(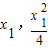 ),B(
),B(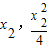 ),M(
),M(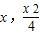 )
)
直线方程代入抛物线方程可得x2-4kx-4=0
∴x1+x2=4k,x1x2=-4
∵MA⊥MB,∴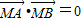
∴(x1-x)(x2-x)+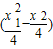
 =0
=0
∵M不与A,B重合,∴(x1-x)(x2-x)≠0
∴1+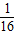 (x1+x)(x2+x)=0
(x1+x)(x2+x)=0
∴x1x2+(x1+x2)x+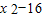 =0
=0
∴
∴△=16k2-48≥0
∴k≤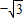 或k≥
或k≥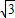 .
.
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
(2)直线方程代入抛物线方程,利用韦达定理及MA⊥MB,建立方程,即可求直线l的斜率k的取值范围.
解答:解:(1)∵|AF|=2,∴由抛物线的定义,可得1+
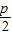 =2,∴p=2
=2,∴p=2∴抛物线C的方程为x2=4y;
(2)抛物线C的焦点为F(0,1),设直线l的方程为y=kx+1,A(
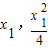 ),B(
),B(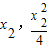 ),M(
),M(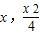 )
)直线方程代入抛物线方程可得x2-4kx-4=0
∴x1+x2=4k,x1x2=-4
∵MA⊥MB,∴
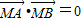
∴(x1-x)(x2-x)+
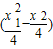
 =0
=0∵M不与A,B重合,∴(x1-x)(x2-x)≠0
∴1+
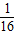 (x1+x)(x2+x)=0
(x1+x)(x2+x)=0∴x1x2+(x1+x2)x+
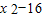 =0
=0∴

∴△=16k2-48≥0
∴k≤
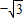 或k≥
或k≥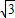 .
.点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 的焦点F作倾斜角为
的焦点F作倾斜角为 的直线交抛物线于A、B两点,使
的直线交抛物线于A、B两点,使 ,过点A作与x轴重直的直线交抛物线于点C,则△BCF的面积是( )
,过点A作与x轴重直的直线交抛物线于点C,则△BCF的面积是( )