题目内容
如图，正方体ABCD—A1B1C1D1的棱长为2，动点E、F在棱A1B1上。点Q是CD的中点，动点P在棱AD上，若EF=1，DP=x，A1E=y(x,y大于零)，则三棱锥P-EFQ的体积( )
| A．与x，y都有关； | B．与x，y都无关； |
| C．与x有关，与y无关； | D．与y有关，与x无关； |
C
解析解：三棱锥P-EFQ的体积与点P到平面EFQ的距离和数据线EFQ的面积有关，
由图形可知，平面EFQ与平面CDA1B1是同一平面，故点P到平面EFQ的距离
是P到平面CDA1B1的距离，且该距离就是P到线段A1D的距离，此距离只与x有关，
因为EF=1，点Q到EF 的距离为线段B1C的长度，为定值，
综上可知所求三棱锥的体积只与x有关，与y无关．
故选C．
练习册系列答案
相关题目
在正方体
中，E是棱
的中点，则BE与平面
所成角的正弦值为
A． | B． | C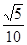． | D． |
若一个二面角的两个半平面与另一个二面角的两个半平面互相垂直，则这两个二面角的大小 ( )
| A．相等 | B．互补 | C．相等或互补 | D．无法确定 |
、
为两条不重合的直线，
、
为两个不重合的平面，则下列命题中，真命题的个数是（ ）两二面角的的两个半平面分别垂直，则这两个二面角的大小关系是（ ）
| A．一定相等 | B．一定互补 |
| C．一定相等或互补 | D．以上都不对 |
如果直线l，m与平面α、β、γ满足β∩γ＝l，，
，
，那么必有（ ）
| A．m//β且l⊥m | B．α//β且α⊥γ |
| C．α⊥β且m//γ | D．α⊥γ且l⊥m |
，PA⊥平面ABC，则四面体P-ABC中共有（ ）个直角三角形
在空间内，可以确定一个平面的条件是 （ ）
| A．两两相交的三条直线 | B．三条直线，其中的一条与另外两条直线分别相交 |
| C．三个点 | D．三条直线，它们两两相交，但不交于同一点 |