题目内容
在300米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( )
分析:如图,设AB为山,CD为塔,Rt△ABD中利用正弦的定义,算出BD=200
米.在△BCD中,得到∠C=120°、∠DBC=30°,利用正弦定理列式,解出CD=200米,即塔高为为200米.
| 3 |
解答:解:如图,设AB为山,CD为塔,则
Rt△ABD中,∠ADB=60°,AB=300米
∴sin∠ADB=
=
,得BD=
=200
米
在△BCD中,∠BDC=90°-60°=30°,∠DBC=60°-30°=30°,
∴∠C=180°-30°-30°=120°
由正弦定理,得
=
,
∴CD=
×sin30°=200米,即塔高为为200米
故选:A

Rt△ABD中,∠ADB=60°,AB=300米
∴sin∠ADB=
| AB |
| BD |
| ||
| 2 |
| 300 | ||||
|
| 3 |
在△BCD中,∠BDC=90°-60°=30°,∠DBC=60°-30°=30°,
∴∠C=180°-30°-30°=120°
由正弦定理,得
| BD |
| sin120° |
| CD |
| sin30° |
∴CD=
| BD |
| sin120° |
故选:A
点评:本题给出实际问题,求距离山远处的一个塔的高,着重考查了直角三角形三角函数的定义和正弦定理解三角形等知识,属于基础题.

练习册系列答案
相关题目
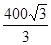 米 C.
200
米 C.
200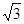 米 D.
米 D. 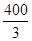 米
米 米 C. 200
米 C. 200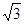 米 D.
米 D.  米
米 米
米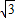 米
米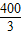 米
米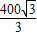 米
米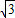 米
米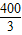 米
米