题目内容
已知命题P：不等式lg[x（1-x）+1]＞0的解集为{x|0＜x＜1}；命题Q：在三角形ABC中，∠A＞∠B是cos2（
+
）＜cos2（
+
）成立的必要而非充分条件，则（ ）
| A |
| 2 |
| π |
| 4 |
| B |
| 2 |
| π |
| 4 |
| A．P真Q假 | B．P且Q为真 | C．P或Q为假 | D．P假Q真 |
由命题P：不等式lg[x（1-x）+1]＞0，可知lg[x（1-x）+1]＞lg1．∴x（1-x）+1＞1，∴0＜x＜1，即不等式的解为{x|0＜x＜1}；所以命题P为真命题．由命题Q知，若cos2（
+
）＜cos2（
+
），即sinA＞sinB，∴∠A＞∠B；反之，在三角形中若∠A＞∠B则必有sinA＞sinB，即cos2（
+
）＜cos2（
+
）成立，所以命题Q为假命题．
故选A．
| A |
| 2 |
| π |
| 4 |
| B |
| 2 |
| π |
| 4 |
| A |
| 2 |
| π |
| 4 |
| B |
| 2 |
| π |
| 4 |
故选A．
练习册系列答案
相关题目
已知命题P：不等式lg[x（1-x）+1]＞0的解集为{x|0＜x＜1}；命题Q：在三角形ABC中，∠A＞∠B是cos2（
+
）＜cos2（
+
）成立的必要而非充分条件，则（ ）
| A |
| 2 |
| π |
| 4 |
| B |
| 2 |
| π |
| 4 |
| A、P真Q假 | B、P且Q为真 |
| C、P或Q为假 | D、P假Q真 |
+
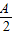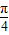）＜cos2（
+
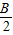）成立的必要而非充分条件，则（ ）