题目内容
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
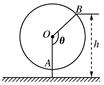
(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?

(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?
(1)以圆心O为原点,建立如图所示的平面直角坐标系,
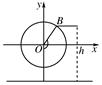
则以Ox为始边,OB为终边的角为θ-,
故点B的坐标为
(4.8cos,4.8sin),
∴h=5.6+4.8sin.
(2)点A在圆上转动的角速度是,故t秒转过的弧度数为t,
∴h=5.6+4.8sin,t∈[0,+∞).
到达最高点时,h=10.4 m.
由sin=1
得t-=,
∴t=30
∴缆车到达最高点时,用的时间最少为30秒

则以Ox为始边,OB为终边的角为θ-,
故点B的坐标为
(4.8cos,4.8sin),
∴h=5.6+4.8sin.
(2)点A在圆上转动的角速度是,故t秒转过的弧度数为t,
∴h=5.6+4.8sin,t∈[0,+∞).
到达最高点时,h=10.4 m.
由sin=1
得t-=,
∴t=30
∴缆车到达最高点时,用的时间最少为30秒
略

练习册系列答案
相关题目
 的终边与单位圆的交点的坐标是 .
的终边与单位圆的交点的坐标是 . 的终边上,且|OP|=2,则点P的坐标是( )
的终边上,且|OP|=2,则点P的坐标是( )



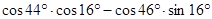 的结果等于
的结果等于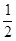
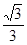
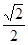

 的最小正周期
的最小正周期
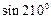 的值为 ( )
的值为 ( )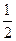 B
B 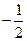 C
C 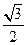 D
D 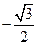
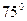 ,半径等于
,半径等于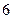 ,则扇形的面积为 .
,则扇形的面积为 .