题目内容
已知直线l1:x+my+5=0和直线l2: x+ny+p=0,则l1、l2关于y轴对称的充要条件是( )
| A.= | B.p=-5 |
| C.m=-n且p=-5 | D.=-且p=-5 |
C
求出直线l1关于y轴对称的直线方程,其与l2:x+ny+p=0,必为同一条直线,利用同一性找出对应的系数相等即可
解:直线l1关于y轴对称的直线方程为(-x)+my+5=0,
即x-my-5=0,与l2比较,
∴m=-n且p=-5.
反之亦验证成立.
故应选C.
解:直线l1关于y轴对称的直线方程为(-x)+my+5=0,
即x-my-5=0,与l2比较,
∴m=-n且p=-5.
反之亦验证成立.
故应选C.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
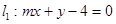 和直线
和直线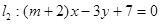 与两坐标轴围成的四边
与两坐标轴围成的四边 的值是( )
的值是( ) 
 或
或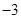
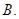
 或
或 

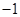 或
或 

 或
或 
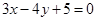 关于
关于 轴对称的直线方程为( )
轴对称的直线方程为( )



 平行且距离等于
平行且距离等于 的直线
的直线 方程.
方程. 
 与
与 轴、
轴、 轴分别交于
轴分别交于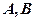 两点,若动点
两点,若动点 在线段
在线段 上,则
上,则 的最大值为
的最大值为  .
. 
 .
. 
 .
.
 .
.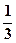
 一条光线从点P(6,4)射出,经y轴反射后经过点Q(3,10),求入射光线和反射光线所在直线方程。 (12分)
一条光线从点P(6,4)射出,经y轴反射后经过点Q(3,10),求入射光线和反射光线所在直线方程。 (12分)