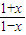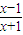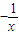题目内容
设 ,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2009(x)=
- A.

- B.

- C.x
- D.

A
分析:根据fk+1(x)=f(fk(x)),分别求出f1(x),f2(x),f3(x),f4(x),f5(x)发现函数列{fK(x)}是以4为周期的函数列,进而可知f2009(x)=f1(x),求得答案.
解答:依题意得f1(x)= ,f2(x)=-
,f2(x)=- ,f3(x)=
,f3(x)= ,f4(x)=x,f5(x)=
,f4(x)=x,f5(x)= =f1(x)
=f1(x)
即函数列{fK(x)}是以4为周期的函数列,注意到2009=4×502+1,因此f2009(x)=f1(x)=
故选A.
点评:本题主要考查函数的周期性.解本题关键是找出函数列的周期.
分析:根据fk+1(x)=f(fk(x)),分别求出f1(x),f2(x),f3(x),f4(x),f5(x)发现函数列{fK(x)}是以4为周期的函数列,进而可知f2009(x)=f1(x),求得答案.
解答:依题意得f1(x)=
 ,f2(x)=-
,f2(x)=- ,f3(x)=
,f3(x)= ,f4(x)=x,f5(x)=
,f4(x)=x,f5(x)= =f1(x)
=f1(x)即函数列{fK(x)}是以4为周期的函数列,注意到2009=4×502+1,因此f2009(x)=f1(x)=

故选A.
点评:本题主要考查函数的周期性.解本题关键是找出函数列的周期.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2012(x)=( )
,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2012(x)=( )