题目内容
在数列中，对于任意自然数，都有a1+a2+…+an=2n-1，则a12+a22+…+an2=
．
| 4n-1 |
| 3 |
| 4n-1 |
| 3 |
分析：利用Sn与an关系，得出an2=4 n-1， 得出数列{an2}是以4为公比的等比数列，利用等比数列求和公式计算即可．
解答：解：∵a1+a2+…+an=2n-1 ①∴a1+a2+…+an+1+an+1=2n+1-1②，②-①得a n+1=2n∴an2=4 n-1，数列{an2}是以4为公比的等比数列，由a1=2-1=1，得a12=1
由等比数列求和公式得a12+a22+…+an2=
=
故答案为：
．
由等比数列求和公式得a12+a22+…+an2=
| 1-4n |
| 1-4 |
| 4n-1 |
| 3 |
故答案为：
| 4n-1 |
| 3 |
点评：本题考查了Sn与an关系的具体应用，等比数列的定义，判断，求和公式．
练习册系列答案
相关题目
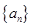中，对于任意
，等式：
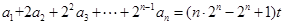恒成立，其中常数
．
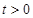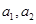的值；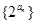 
为等比数列；
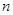的不等式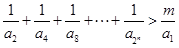
的解集为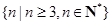
，试求实数
的取值范围．