题目内容
若函数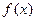 的定义域为R, 则“函数
的定义域为R, 则“函数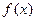 为奇函数”是“函数
为奇函数”是“函数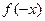 奇函数”的( )
奇函数”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分又非必要条件 |
C
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
奇函数 在区间
在区间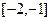 上是减函数,且有最小值
上是减函数,且有最小值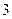 ,那么
,那么 在区间
在区间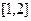 为( )
为( )
A.增函数且最小值为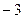 | B.增函数且最大值为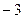 |
C.减函数且最小值为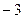 | D.减函数且最大值为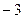 |
若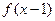 的定义域为[1,2],则
的定义域为[1,2],则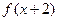 的定义域为( )
的定义域为( )
| A.[0,1] | B.[2,3] | C.[-2,-1] | D.无法确定 |
定义在 上的函数
上的函数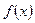 是偶函数,且
是偶函数,且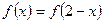 ,若
,若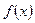 在区间
在区间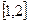 是减函数,则函数
是减函数,则函数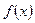 ( )
( )
A.在区间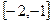 上是增 上是增 函数,区间 函数,区间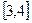 上是增函数 上是增函数 |
B.在区间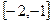 上是增函数,区间 上是增函数,区间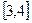 上是减函数 上是减函数 |
C.在区间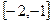 上是减函数,区间 上是减函数,区间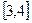 上是增函数 上是增函数 |
D.在区间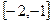 上是减函数,区间 上是减函数,区间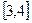 上是减函数 上是减函数 |
定义在R上的函数 上是增函数,且函数
上是增函数,且函数 的图象的对称轴是直线
的图象的对称轴是直线 则
则
A. | B. | C. | D. |
函数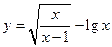 的定义域为 ( )
的定义域为 ( )
A.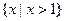 | B.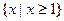 |
C.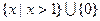 | D.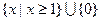 |
函数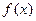 的定义域为R,若
的定义域为R,若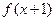 与
与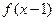 都是奇函数,则( )
都是奇函数,则( )
A.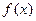 是偶函数 是偶函数 | B.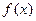 是奇函数 是奇函数 |
C.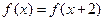 | D.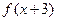 是奇函数 是奇函数 |
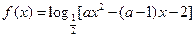 的值域为R,且
的值域为R,且 在(2,5)上是减函数,则实数a的取值范围是( )
在(2,5)上是减函数,则实数a的取值范围是( )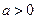
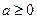
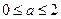
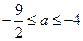
 的定义域为
的定义域为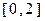 ,则
,则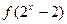 的定义域为 ( )
的定义域为 ( )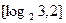
 C.
C.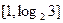 D
D .[1,2]
.[1,2]