题目内容
已知函数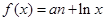 ,其中实数a为常数.
,其中实数a为常数.
(I)当a=-l时,确定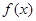 的单调区间:
的单调区间:
(II)若f(x)在区间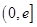 (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值;
(Ⅲ)当a=-1时,证明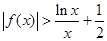 .
.
【答案】
(Ⅰ) 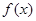 在区间
在区间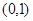 上为增函数,在区间
上为增函数,在区间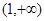 上为减函数.(Ⅱ)
上为减函数.(Ⅱ)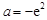 .
(Ⅲ) 见解析.
.
(Ⅲ) 见解析.
【解析】
试题分析:(Ⅰ)通过求导数,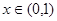 时,
时, 
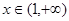 时,
时,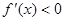 ,单调函数的单调区间.
,单调函数的单调区间.
(Ⅱ)遵循“求导数,求驻点,讨论区间导数值正负,确定端点函数值,比较大小”等步骤,得到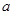 的方程.注意分①
的方程.注意分①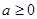 ;②
;② ;③
;③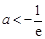 ,等不同情况加以讨论.
,等不同情况加以讨论.
(Ⅲ) 根据函数结构特点,令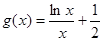 ,利用“导数法”,研究
,利用“导数法”,研究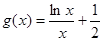 有最大值
有最大值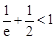 ,根据
,根据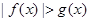 , 得证.
, 得证.
试题解析:(Ⅰ)当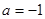 时,
时,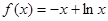 ,∴
,∴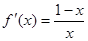 ,又
,又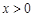 ,所以
,所以
当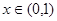 时,
时, 
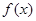 在区间
在区间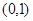 上为增函数,
上为增函数,
当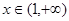 时,
时,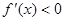 ,
,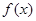 在区间
在区间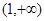 上为减函数,
上为减函数,
即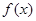 在区间
在区间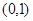 上为增函数,在区间
上为增函数,在区间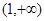 上为减函数. 4分
上为减函数. 4分
(Ⅱ)∵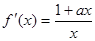 ,①若
,①若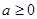 ,∵
,∵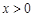 ,则
,则 在区间
在区间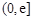 上恒成立,
上恒成立,
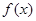 在区间
在区间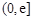 上为增函数,
上为增函数,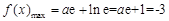 ,∴
,∴ ,舍去;
,舍去;
②当 时,∵
时,∵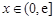 ,∴
,∴
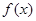 在区间
在区间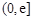 上为增函数,
上为增函数,
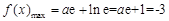 ,∴
,∴ ,舍去;
,舍去;
③若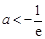 ,当
,当 时,
时,
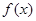 在区间
在区间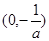 上为增函数,
上为增函数,
当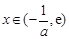 时,
时,
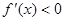 ,
,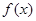 在区间
在区间 上为减函数,
上为减函数,
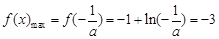 ,∴
,∴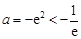 .
.
综上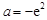 .
9分
.
9分
(Ⅲ) 由(Ⅰ)知,当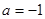 时,
时,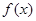 有最大值,最大值为
有最大值,最大值为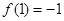 ,即
,即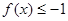 ,
,
所以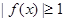 ,
10分
,
10分
令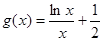 ,则
,则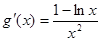 ,
,
当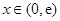 时,
时,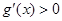 ,
,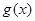 在区间
在区间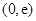 上为增函数,
上为增函数,
当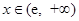 时,
时,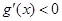 ,
,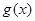 在区间
在区间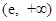 上为减函数,
上为减函数,
所以当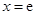 时,
时,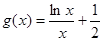 有最大值
有最大值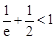 ,12分
,12分
所以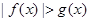 ,
,
即 .
13分
.
13分
考点:应用导数研究函数的单调性、极值、最值、证明不等式.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
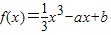 ,其中实数a,b是常数.
,其中实数a,b是常数.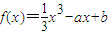 ,其中实数a,b是常数.
,其中实数a,b是常数.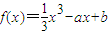 ,其中实数a,b是常数.
,其中实数a,b是常数.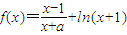 ,其中实数a≠1.
,其中实数a≠1.