题目内容
若要(x-1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,则m的一个可能值是
- A.3
- B.

- C.2
- D.
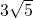
A
分析:先由圆的方程找出圆心A的坐标和圆的半径,然后根据图形可知当圆心到直线的距离d大于1小于3时,(x-1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,所以利用点到直线的距离公式表示出点A到直线2x+y+m=0的距离d,令d大于1小于3列出关于m的不等式,求出不等式的解集即可得到m的范围,根据m的范围即可判断出正确答案.
解答: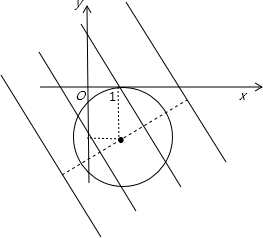 解:由圆的方程(x-1)2+(y+2)2=4,得到圆心A的坐标为(1,-2),圆的半径为2,
解:由圆的方程(x-1)2+(y+2)2=4,得到圆心A的坐标为(1,-2),圆的半径为2,
设圆心A到直线2x+y+m=0的距离为d,
据图形可知:当1<d<3时,圆上恰有两点到直线2x+y+m=0的距离等于1,
由d=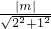 ,代入得:1<
,代入得:1<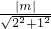 <3,
<3,
解得: <m<3
<m<3 ,
,
因为 <3<3
<3<3 ,所以m可能等于3.
,所以m可能等于3.
故选A
点评:此题考查学生灵活运用点到直线的距离公式化简求值,考查了数形结合的数学思想,是一道中档题.
分析:先由圆的方程找出圆心A的坐标和圆的半径,然后根据图形可知当圆心到直线的距离d大于1小于3时,(x-1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,所以利用点到直线的距离公式表示出点A到直线2x+y+m=0的距离d,令d大于1小于3列出关于m的不等式,求出不等式的解集即可得到m的范围,根据m的范围即可判断出正确答案.
解答:
 解:由圆的方程(x-1)2+(y+2)2=4,得到圆心A的坐标为(1,-2),圆的半径为2,
解:由圆的方程(x-1)2+(y+2)2=4,得到圆心A的坐标为(1,-2),圆的半径为2,设圆心A到直线2x+y+m=0的距离为d,
据图形可知:当1<d<3时,圆上恰有两点到直线2x+y+m=0的距离等于1,
由d=
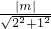 ,代入得:1<
,代入得:1<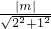 <3,
<3,解得:
 <m<3
<m<3 ,
,因为
 <3<3
<3<3 ,所以m可能等于3.
,所以m可能等于3.故选A
点评:此题考查学生灵活运用点到直线的距离公式化简求值,考查了数形结合的数学思想,是一道中档题.

练习册系列答案
相关题目
若要(x-1)2+(y+2)2=4上恰有两个点到直线2x+y+m=0的距离等于1,则m的一个可能值是( )
| A、3 | ||
B、
| ||
| C、2 | ||
D、3
|
若p:|x+1|>2和q:
>0,则¬p是¬q( )条件.
| 1 |
| x2+3x-4 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
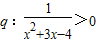 ,则¬p是¬q( )条件.
,则¬p是¬q( )条件.
