题目内容
与椭圆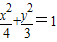
具有相同的离心率且过点（2，-
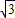）的椭圆的标准方程是 ．
【答案】分析：当椭圆的焦点在x轴上，设椭圆方程为：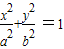
（a＞b＞0），利用椭圆
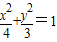的方程得出离心率，列出关于a，b关系，将点的坐标代入方程求出a，b即可得到结论．当椭圆的焦点在y轴上时同样得到椭圆的解析式．
解答：解：椭圆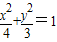
的离心率e=
，
①当椭圆的焦点在x轴上，由题设椭圆方程为：
（a＞b＞0）
由题得：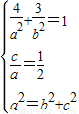
⇒
．
故椭圆方程为：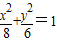
．
②当椭圆的焦点在y轴上，由题设椭圆方程为：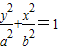
（a＞b＞0）
由题得：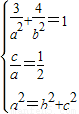
⇒
．
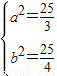故椭圆方程为：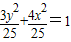
．
故答案为：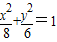
或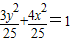 
点评：本题考查椭圆的标准方程、圆标准方程，以及椭圆的简单性质的应用．关键是灵活运用椭圆简单性质解决数学问题的能力．
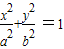（a＞b＞0），利用椭圆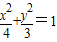的方程得出离心率，列出关于a，b关系，将点的坐标代入方程求出a，b即可得到结论．当椭圆的焦点在y轴上时同样得到椭圆的解析式．解答：解：椭圆
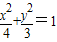的离心率e=，①当椭圆的焦点在x轴上，由题设椭圆方程为：
（a＞b＞0）由题得：
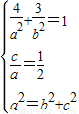⇒．故椭圆方程为：
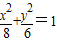．②当椭圆的焦点在y轴上，由题设椭圆方程为：
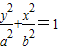（a＞b＞0）由题得：
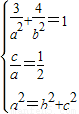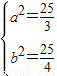⇒．故椭圆方程为：
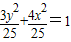．故答案为：
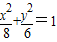或 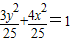点评：本题考查椭圆的标准方程、圆标准方程，以及椭圆的简单性质的应用．关键是灵活运用椭圆简单性质解决数学问题的能力．
练习册系列答案
相关题目
具有相同的离心率且过点(2，－
)的椭圆的标准方程是________
具有相同的离心率且过点（2，-
）的椭圆的标准方程是________．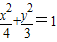
具有相同的离心率且过点（2，-
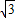）的椭圆的标准方程是 ．
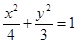具有相同的离心率且过点（2，-
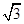）的椭圆的标准方程是_____ 。