题目内容
设 ,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )
,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )A.1
B.2
C.3
D.4
【答案】分析:由幂函数在(0,+∞)的单调性缩小a的范围,再由幂函数的奇偶性即可确定a的值
解答:解:∵y=xa在(0,+∞)上单调递减
∴a<0
∴a的可能取值为-3,-2,-1,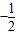
又∵y=xa为奇函数
当a=-2时,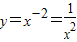 是偶函数;
是偶函数;
当a=- 时,
时, 是非奇非偶函数不合题意
是非奇非偶函数不合题意
∴a=-3或a=-1
∴满足题意的a的值有2个
故选B
点评:本题考查幂函数的性质,要注意幂函数的指数a与第一象限内的图象的单调性之间的关系,a<0是单调递减,a>0时单调递增;同时要求会判断幂函数的奇偶性.属简单题
解答:解:∵y=xa在(0,+∞)上单调递减
∴a<0
∴a的可能取值为-3,-2,-1,
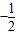
又∵y=xa为奇函数
当a=-2时,
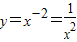 是偶函数;
是偶函数;当a=-
 时,
时, 是非奇非偶函数不合题意
是非奇非偶函数不合题意∴a=-3或a=-1
∴满足题意的a的值有2个
故选B
点评:本题考查幂函数的性质,要注意幂函数的指数a与第一象限内的图象的单调性之间的关系,a<0是单调递减,a>0时单调递增;同时要求会判断幂函数的奇偶性.属简单题

练习册系列答案
相关题目
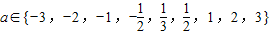 ,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )
,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( ) ,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )
,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( ) ,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )
,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )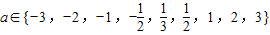 ,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )
,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )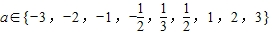 ,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )
,则使y=xa为奇函数且在(0,+∞)上单调递减的a值的个数为( )