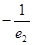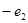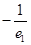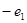题目内容
如下图,一单位正方体形积木,平放于桌面上,并且在其上方放置若干个小正方体形积木摆成塔形,其中上面正方体中下底面的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积之和超过8.8,则正方体的个数至少是 ( )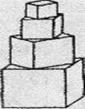
A.6 8.7 C.8 D. 10
A
解析试题分析:依题意,由下往上数,正方体的棱长依次为:1、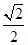 、
、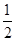 、
、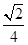
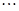 成等比数列,公比是
成等比数列,公比是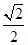 .每一层正方体暴露在外的部分都是由四个侧面及上面的四个全等的等腰直角三角形构成.设正方体棱长为
.每一层正方体暴露在外的部分都是由四个侧面及上面的四个全等的等腰直角三角形构成.设正方体棱长为 ,则上面暴露的等腰直角三角形边长为
,则上面暴露的等腰直角三角形边长为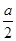 .该层正方体暴露的面积
.该层正方体暴露的面积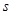 与棱长
与棱长 的关系是:
的关系是: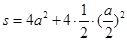
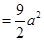 .若正方体个数为
.若正方体个数为 ,则暴露的总面积为:
,则暴露的总面积为: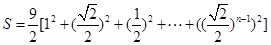
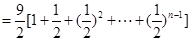
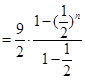
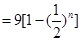 >8.8 所以
>8.8 所以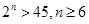 .
.
考点:等比数列前n项和公式

练习册系列答案
相关题目
已知数列 的前
的前 项的和
项的和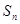 满足
满足 ,则数列
,则数列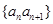 的前
的前 项的和为( )
项的和为( )
A.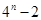 | B.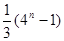 | C.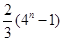 | D.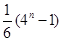 |
在各项都为正数的等比数列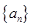 中,
中,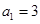 ,前三项的和为
,前三项的和为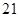 ,则
,则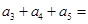 ( )
( )
A.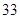 | B.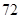 | C. | D.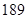 |
正项等比数列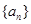 中,
中, 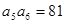 ,则
,则 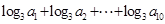 的值是( )
的值是( )
| A.2 | B.5 | C.10 | D.20 |
在正项等比数列{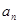 }中,
}中,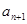 <
<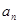 ,
,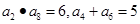 ,则
,则 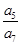 = ( )
= ( )
A.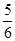 | B.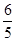 |
C.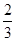 | D.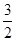 |
在等比数列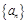 中,若
中,若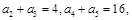 则
则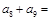 ( )
( )
| A.128 | B.-128 | C.256 | D.-256 |
已知数列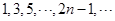 则
则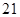 是这个数列的
是这个数列的
| A.第10项 | B.第11项 | C.第12项 | D.第21项 |
数列 为等比数列,且
为等比数列,且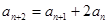 ,
,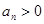 ,则该数列公比
,则该数列公比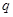 =( )
=( )
| A.1 | B.2 | C.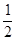 | D. |
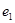 的椭圆与离心率为
的椭圆与离心率为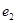 的双曲线有相同的焦点,且椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离依次构成等比数列,则
的双曲线有相同的焦点,且椭圆长轴的端点、短轴的端点、焦点到双曲线的一条渐近线的距离依次构成等比数列,则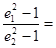 ( )
( )