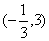题目内容
如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是( )
A.arcsin
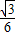
B.arccos

C.arcsin
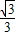
D.arccos

【答案】分析:先求球的半径,确定小圆中ABC的特征,作出直线OA与截面ABC所成的角,然后解三角形求出直线OA与截面ABC所成的角,即可.
解答: 解:表面积为48π的球面,它的半径是R,则48π=4πR2,R=2
解:表面积为48π的球面,它的半径是R,则48π=4πR2,R=2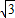 ,
,
因为 AB=2,BC=4,∠ABC=60°,所以∠BAC=90°,BC为小圆的直径,
则平面OBC⊥平面ABC,D为小圆的圆心,
所以OD⊥平面ABC,∠OAD就是直线OA与截面ABC所成的角,
OD=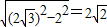 ,
,
∴AD=2,cos∠OAD= ,
,
故选D.
点评:本题考查球的有关计算问题,直线与平面所成的角,考查学生空间想象能力,逻辑思维能力,是中档题.
解答:
 解:表面积为48π的球面,它的半径是R,则48π=4πR2,R=2
解:表面积为48π的球面,它的半径是R,则48π=4πR2,R=2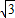 ,
,因为 AB=2,BC=4,∠ABC=60°,所以∠BAC=90°,BC为小圆的直径,
则平面OBC⊥平面ABC,D为小圆的圆心,
所以OD⊥平面ABC,∠OAD就是直线OA与截面ABC所成的角,
OD=
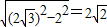 ,
,∴AD=2,cos∠OAD=
 ,
,故选D.
点评:本题考查球的有关计算问题,直线与平面所成的角,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目

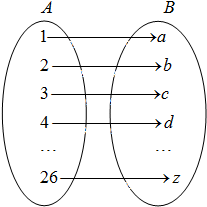 设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=
设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=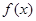 的定义域为[—2,
的定义域为[—2,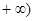 ,部分对应值如下表,
,部分对应值如下表,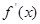 为
为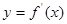 的图象如右图所示:
的图象如右图所示: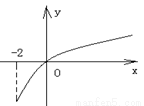
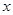
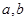 满足
满足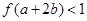 ,则
,则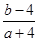 的取值范围是
( )
的取值范围是
( )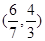 B.
B.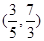 C.
C.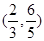 D.
D.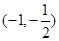
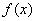 的定义域为[—2,
的定义域为[—2,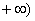 ,部分对应值如下表,
,部分对应值如下表,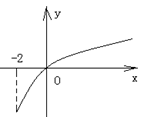
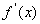 为
为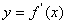 的图象如右图所示:
的图象如右图所示: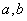 满足
满足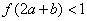 ,则
,则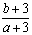 的取值范围是 (
)
的取值范围是 (
)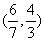 B.
B.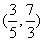 C.
C.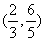 D.
D.