题目内容
19.有以下四个命题,其中真命题的个数为( )①△ABC中,“A>B”是“sinA>sinB”的充要条件;
②若命题p:?x∈R,sinx≤1,则¬p:?x∈R,sinx<1;
③函数y=3sin(2x-$\frac{π}{6}$)+2的单调递减区间是[$\frac{π}{3}$+2kπ,$\frac{5}{6}$π+2kπ](k∈z);
④若函数f(x)=x2+2x+2a与g(x)=|x-1|+|x+a|有相同的最小值,则$\int_1^a{f(x)}dx$=$\frac{28}{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据正弦定理,可判断①;写出原命题的否定,可判断②;求出函数的单调区间,可判断③,求出a值,进而求出积分,可判断④
解答 解:①△ABC中,“A>B”?“a>b”?“2RsinA>2RsinB”?“sinA>sinB”,故“A>B”是“sinA>sinB”的充要条件,即①是真命题;
②若命题p:?x∈R,sinx≤1,则¬p:?x∈R,sinx>1,故②是假命题;
③由2x-$\frac{π}{6}$∈[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ](k∈z)得:x∈[$\frac{π}{3}$+kπ,$\frac{5}{6}$π+kπ](k∈z);
即函数y=3sin(2x-$\frac{π}{6}$)+2的单调递减区间是[$\frac{π}{3}$+kπ,$\frac{5}{6}$π+kπ](k∈z),故③是假命题;
④若函数f(x)=x2+2x+2a的最小值为:2a-1,
函数g(x)=|x-1|+|x+a|的最小值为:|a+1|,
由2a-1=|a+1|得:a=2,
则$\int_1^a{f(x)}dx$=${∫}_{1}^{2}({x}^{2}+2x+4)dx$=$(\frac{1}{3}×{2}^{3}+{2}^{2}+4×2)$-$(\frac{1}{3}×{1}^{3}+{1}^{2}+4×1)$=$\frac{28}{3}$,故④是真命题;
故真命题的个数为2个,
故选:B.
点评 本题以命题的真假判断为载体考查了正弦定理,全称命题的否定,正弦函数的单调性,函数的最值,积分等知识点,难度中档.

练习册系列答案
相关题目
10.若集合A={y|y=2x},B={x|x2-2x-3>0,x∈R},那么A∩B=( )
| A. | (0,3] | B. | [-1,3] | C. | (3,+∞) | D. | (0,-1)∪(3,+∞) |
7.如图所示,三视图表示的几何体是( )
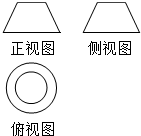

| A. | 圆台 | B. | 棱台 | C. | 棱柱 | D. | 圆锥 |
4.如图是函数f(x)=Acos($\frac{2}{3}$πx+φ)-1(A>0,|φ|<$\frac{π}{2}$)的图象的一部分,则f(2015)=( )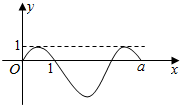

| A. | 1 | B. | 2 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -3 |
8.已知集合M={-2,-1,0,1},N={x|$\frac{1}{2}$≤2x≤4},x∈Z},则M∩N=( )
| A. | M={-2,-1,0,1,2} | B. | M={-1,0,1,2} | C. | M={-1,0,1} | D. | M={0,1} |