题目内容
给出以下几个命题,正确的是①函数f(x)=
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
②已知Sn是等差数列{an},n∈N*的前n项和,若S7>S5,则S9>S3;
③函数f(x)=x|x|+px+q(x∈R)为奇函数的充要条件是q=0;
④已知a,b,m均是正数,且a<b,则
| a+m |
| b+m |
| a |
| b |
分析:根据函数性质对①②③④分别进行判断即可.
解答:解:①对函数f(x)进行变形
=
=
-
∴函数的对称中心为(-
,
)
∴①错误.
②∵S7>S5
a6+a7>0
S9-S3=a9+a8+a7+a6+a5+a4
∵{an}是等差数列
∴a9+a8,a7+a6,a5+a4也为等差数列
且三者之和为2(a7+a6)>0
∴②为真
③当f(x)为奇函数是f(0)=0
∴q=0,
当q=0时
f(-x)=-x|-x|-px=-(x|x|+px)=-f(x)
∴③正确.
④根据合比性质即可知道④正确.
故答案为②③④.
| x-1 |
| 2x+1 |
| ||||
| 2x+1 |
| 1 |
| 2 |
| ||
| 2x+1 |
∴函数的对称中心为(-
| 1 |
| 2 |
| 1 |
| 2 |
∴①错误.
②∵S7>S5
a6+a7>0
S9-S3=a9+a8+a7+a6+a5+a4
∵{an}是等差数列
∴a9+a8,a7+a6,a5+a4也为等差数列
且三者之和为2(a7+a6)>0
∴②为真
③当f(x)为奇函数是f(0)=0
∴q=0,
当q=0时
f(-x)=-x|-x|-px=-(x|x|+px)=-f(x)
∴③正确.
④根据合比性质即可知道④正确.
故答案为②③④.
点评:本题考查了命题的判断,但更重要的是把握各种函数的性质.

练习册系列答案
相关题目
 对称中心是
对称中心是 ;
; 是等差数列
是等差数列 的前
的前 项和,若
项和,若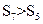 ,则
,则 ;
; 为奇函数的充要条件是
为奇函数的充要条件是 ;[
;[ 均是正数,且
均是正数,且 ,则
,则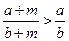 。
。 对称中心是
对称中心是 ;
; 是等差数列
是等差数列 的前
的前 项和 ,若
项和 ,若 ,则
,则 ;
; 为奇函数的充要条件是
为奇函数的充要条件是 ;
; 均是正数,且
均是正数,且 ,则
,则 。
。