题目内容
已知椭圆 的上焦点为F,左、右顶点分别为B1,B2,下顶点为A,直线AB2与直线B1F交于点P,若
的上焦点为F,左、右顶点分别为B1,B2,下顶点为A,直线AB2与直线B1F交于点P,若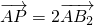 ,则椭圆的离心率为
,则椭圆的离心率为
- A.

- B.

- C.

- D.

D
分析:先写出直线AB2与直线B1F的方程,联立方程组求出交点P的坐标,B2为AP的中点,可得a与c的关系,进而求出离心率.
解答:由题意知,A(0,-a)、F (0,c)、B1(-b,0)、B2(b,0),B2为AP的中点.
AB2方程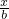 -
-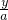 =1,即 ax-by-ab=0 ①,B1F方程
=1,即 ax-by-ab=0 ①,B1F方程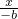 +
+ =1,即 cx-by+bc=0 ②,
=1,即 cx-by+bc=0 ②,
将①②联立方程组可求得点P的坐标(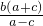 ,
,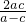 ),
),
再由中点公式得:2b=0+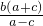 ,0=-a+
,0=-a+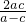 ,
,
∴a=3c,
∴e= =
= .
.
故答案选 D
点评:本题考查椭圆的性质及求2条直线的交点坐标.
分析:先写出直线AB2与直线B1F的方程,联立方程组求出交点P的坐标,B2为AP的中点,可得a与c的关系,进而求出离心率.
解答:由题意知,A(0,-a)、F (0,c)、B1(-b,0)、B2(b,0),B2为AP的中点.
AB2方程
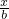 -
-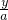 =1,即 ax-by-ab=0 ①,B1F方程
=1,即 ax-by-ab=0 ①,B1F方程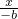 +
+ =1,即 cx-by+bc=0 ②,
=1,即 cx-by+bc=0 ②,将①②联立方程组可求得点P的坐标(
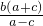 ,
,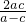 ),
),再由中点公式得:2b=0+
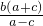 ,0=-a+
,0=-a+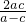 ,
,∴a=3c,
∴e=
 =
= .
.故答案选 D
点评:本题考查椭圆的性质及求2条直线的交点坐标.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
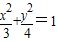 的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= .
的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= . 的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= .
的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= .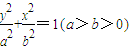 的上焦点为F,左、右顶点分别为B1,B2,下顶点为A,直线AB2与直线B1F交于点P,若
的上焦点为F,左、右顶点分别为B1,B2,下顶点为A,直线AB2与直线B1F交于点P,若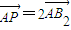 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



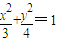 的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= .
的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= . 的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= .
的上焦点为F,直线x+y+1=0和x+y-1=0与椭圆相交于点A,B,C,D,则AF+BF+CF+DF= .