题目内容
定义在![]() 上的可导函数
上的可导函数![]() ,已知
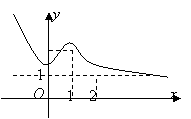
,已知![]() 的图象如图,
的图象如图,![]() 的增区间是( )
的增区间是( )
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
B

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
题目内容
定义在![]() 上的可导函数
上的可导函数![]() ,已知
,已知![]() 的图象如图,
的图象如图,![]() 的增区间是( )
的增区间是( )
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案