题目内容
设A是满足下列两个条件的无穷数列{an}的集合:
①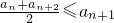 ; ②an≤M.其中n∈N*,M是与n无关的常数.
; ②an≤M.其中n∈N*,M是与n无关的常数.
(Ⅰ)若{an}是等差数列,Sn是其前n项的和,a3=4,S3=18,证明:{Sn}∈A;
(Ⅱ)对于(Ⅰ)中数列{an},正整数n1,n2,…,nt…(t∈N*)满足7<n1<n2<…<nt<…(t∈N*),并且使得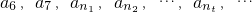 成等比数列. 若bm=10m-nm(m∈N*),则{bm}∈A是否成立?若成立,求M的取值范围,若不成立,请说明理由;
成等比数列. 若bm=10m-nm(m∈N*),则{bm}∈A是否成立?若成立,求M的取值范围,若不成立,请说明理由;
(Ⅲ)设数列{cn}的各项均为正整数,且{cn}∈A,证明:cn≤cn+1.
解:(Ⅰ)设等差数列{an}的公差是d,
则a1+2d=4,3a1+3d=18,
解得a1=8,d=-2.,
所以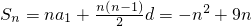 .
.
由 ,
,
得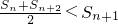 ,适合条件 ①.
,适合条件 ①.
又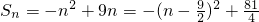 ,
,
所以当n=4或5时,Sn取得最大值20,
即Sn≤20,适合条件 ②.
所以,{Sn}∈A.4分
(Ⅱ)由(Ⅰ)得a1=8,d=-2,
故an=8-2(n-1)=10-2n,
因此a6=-2,a7=-4.
因为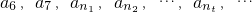 成等比数列,
成等比数列,
故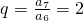 .
.
所以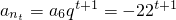 .
.
又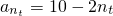 ,所以nt=2t+1+5.
,所以nt=2t+1+5.
从而bm=10m-2m+1-5.
因为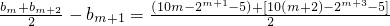 -[10(m+1)-2m+2-5]=-2m<0,
-[10(m+1)-2m+2-5]=-2m<0,
故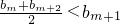 .
.
又b1<b2<b3,并且b3>b4>b5>…,
而b3=10×3-23+1-5=9,
故当m∈N*时,bm≤9.
综上,当m∈N*时,{bm}∈A,此时M的取值范围是[9,+∞).9分
(Ⅲ)假设存在正整数k,使得ck>ck+1成立.
由数列{cn}的各项均为正整数,
可得ck≥ck+1+1,即ck+1≤ck-1.
∵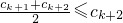 ,
,
∴ck+2≤2ck+1-ck
≤2(ck-1)-ck
=ck-2,
由ck+2≤2ck+1-ck及ck>ck+1,
得ck+2<2ck+1-ck+1=ck+1,
故ck+2≤ck+1-1.
∵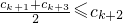 ,
,
∴ck+3≤2ck+2-ck+1≤2(ck+1-1)-ck+1=ck+1-2≤ck-3,
依此类推,可得ck+m≤ck-m(m∈N*).
设ck=p(p∈N*),则当m=p时,有ck+p≤ck-p=0,
这显然与数列{cn}的各项均为正整数矛盾.
所以假设不成立,即对于任意n∈N*,都有cn≤cn+1成立.14分.
分析:(Ⅰ)设等差数列{an}的公差是d,则a1+2d=4,3a1+3d=18,解得a1=8,d=-2,所以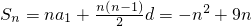 .由此能够证明{Sn}∈A.
.由此能够证明{Sn}∈A.
(Ⅱ)由a1=8,d=-2,知an=8-2(n-1)=10-2n,因此a6=-2,a7=-4.因为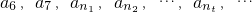 成等比数列,故
成等比数列,故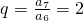 .所以
.所以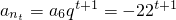 .又
.又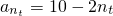 ,所以nt=2t+1+5.从而bm=10m-2m+1-5.由此能求出M的取值范围.
,所以nt=2t+1+5.从而bm=10m-2m+1-5.由此能求出M的取值范围.
(Ⅲ)假设存在正整数k,使得ck>ck+1成立.由数列{cn}的各项均为正整数,可得ck≥ck+1+1即ck+1≤ck-1.因为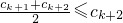 ,所以ck+2≤2ck+1-ck≤ck-2,由此能够推导出对于任意n∈N*,都有cn≤cn+1成立.
,所以ck+2≤2ck+1-ck≤ck-2,由此能够推导出对于任意n∈N*,都有cn≤cn+1成立.
点评:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,考查数列的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答.
则a1+2d=4,3a1+3d=18,
解得a1=8,d=-2.,
所以
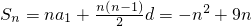 .
.由
 ,
,得
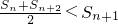 ,适合条件 ①.
,适合条件 ①.又
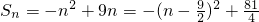 ,
,所以当n=4或5时,Sn取得最大值20,
即Sn≤20,适合条件 ②.
所以,{Sn}∈A.4分
(Ⅱ)由(Ⅰ)得a1=8,d=-2,
故an=8-2(n-1)=10-2n,
因此a6=-2,a7=-4.
因为
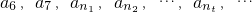 成等比数列,
成等比数列,故
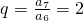 .
.所以
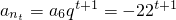 .
.又
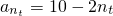 ,所以nt=2t+1+5.
,所以nt=2t+1+5.从而bm=10m-2m+1-5.
因为
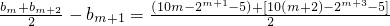 -[10(m+1)-2m+2-5]=-2m<0,
-[10(m+1)-2m+2-5]=-2m<0,故
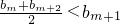 .
.又b1<b2<b3,并且b3>b4>b5>…,
而b3=10×3-23+1-5=9,
故当m∈N*时,bm≤9.
综上,当m∈N*时,{bm}∈A,此时M的取值范围是[9,+∞).9分
(Ⅲ)假设存在正整数k,使得ck>ck+1成立.
由数列{cn}的各项均为正整数,
可得ck≥ck+1+1,即ck+1≤ck-1.
∵
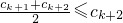 ,
,∴ck+2≤2ck+1-ck
≤2(ck-1)-ck
=ck-2,
由ck+2≤2ck+1-ck及ck>ck+1,
得ck+2<2ck+1-ck+1=ck+1,
故ck+2≤ck+1-1.
∵
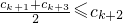 ,
,∴ck+3≤2ck+2-ck+1≤2(ck+1-1)-ck+1=ck+1-2≤ck-3,
依此类推,可得ck+m≤ck-m(m∈N*).
设ck=p(p∈N*),则当m=p时,有ck+p≤ck-p=0,
这显然与数列{cn}的各项均为正整数矛盾.
所以假设不成立,即对于任意n∈N*,都有cn≤cn+1成立.14分.
分析:(Ⅰ)设等差数列{an}的公差是d,则a1+2d=4,3a1+3d=18,解得a1=8,d=-2,所以
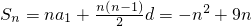 .由此能够证明{Sn}∈A.
.由此能够证明{Sn}∈A.(Ⅱ)由a1=8,d=-2,知an=8-2(n-1)=10-2n,因此a6=-2,a7=-4.因为
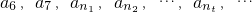 成等比数列,故
成等比数列,故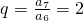 .所以
.所以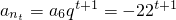 .又
.又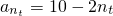 ,所以nt=2t+1+5.从而bm=10m-2m+1-5.由此能求出M的取值范围.
,所以nt=2t+1+5.从而bm=10m-2m+1-5.由此能求出M的取值范围.(Ⅲ)假设存在正整数k,使得ck>ck+1成立.由数列{cn}的各项均为正整数,可得ck≥ck+1+1即ck+1≤ck-1.因为
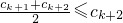 ,所以ck+2≤2ck+1-ck≤ck-2,由此能够推导出对于任意n∈N*,都有cn≤cn+1成立.
,所以ck+2≤2ck+1-ck≤ck-2,由此能够推导出对于任意n∈N*,都有cn≤cn+1成立.点评:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,考查数列的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 ,
, ,设
,设 是
是 中的两个锐角,则下列四个式子中不一定
中的两个锐角,则下列四个式子中不一定 B.
B.
 D.
D.