题目内容
已知各项均为正数的数列{an}满足a1=1,an+1+an•an+1-an=0.
(Ⅰ)求证:数列 是等差数列,并求数列{an}的通项公式;
是等差数列,并求数列{an}的通项公式;
(Ⅱ)求数列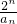 前n项和Sn.
前n项和Sn.
解:(Ⅰ)∵an+1+an•an+1-an=0,∴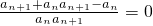 ,
,
∴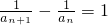 ,
,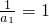 ,
,
∴数列 是以1为首项,1为公差的等差数列.
是以1为首项,1为公差的等差数列.
 ,可得
,可得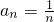 .
.
(Ⅱ)由(Ⅰ)知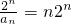 .
.
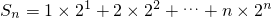 .①
.①
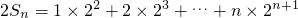 .②
.②
由①-②得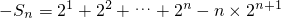 .
.
∴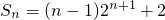 .
.
分析:(I)由于各项均为正数的数列{an}满足a1=1,an+1+an•an+1-an=0,两边同除以anan+1,即可得到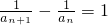 ,转化为等差数列,利用通项公式即可得出;
,转化为等差数列,利用通项公式即可得出;
(II)由(Ⅰ)知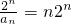 .利用“错位相减法”和等比数列的前n项和公式即可得出.
.利用“错位相减法”和等比数列的前n项和公式即可得出.
点评:熟练掌握等差数列的通项公式、“错位相减法”和等比数列的前n项和公式是解题的关键.
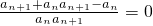 ,
,∴
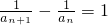 ,
,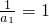 ,
,∴数列
 是以1为首项,1为公差的等差数列.
是以1为首项,1为公差的等差数列. ,可得
,可得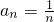 .
.(Ⅱ)由(Ⅰ)知
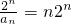 .
.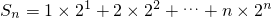 .①
.①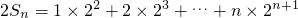 .②
.②由①-②得
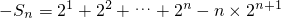 .
.∴
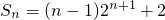 .
.分析:(I)由于各项均为正数的数列{an}满足a1=1,an+1+an•an+1-an=0,两边同除以anan+1,即可得到
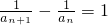 ,转化为等差数列,利用通项公式即可得出;
,转化为等差数列,利用通项公式即可得出;(II)由(Ⅰ)知
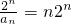 .利用“错位相减法”和等比数列的前n项和公式即可得出.
.利用“错位相减法”和等比数列的前n项和公式即可得出.点评:熟练掌握等差数列的通项公式、“错位相减法”和等比数列的前n项和公式是解题的关键.

练习册系列答案
相关题目
 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明.