题目内容
已知两圆![]() 和
和![]() ,动圆P与⊙O1外切,且与⊙O2内切.
,动圆P与⊙O1外切,且与⊙O2内切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点M(5,0)作直线![]() 与点P的轨迹交于不同两点A、B,试推断是否存在直线
与点P的轨迹交于不同两点A、B,试推断是否存在直线![]() ,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线
,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(Ⅰ)动圆圆心P的轨迹方程是![]()
(Ⅱ)不存在直线![]() 使得线段AB的垂直平分线经过圆心O2.
使得线段AB的垂直平分线经过圆心O2.
解析:
(Ⅰ)由已知,点![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则
|O1O2|=2<![]() ,所以⊙O1内含于⊙O2. (2分)
,所以⊙O1内含于⊙O2. (2分)
设圆P的半径为r,因为动圆P与⊙O1外切,且与⊙O2内切,则
![]() .
.
所以动圆圆心P轨迹是以点![]() 为焦点的椭圆. (4分)
为焦点的椭圆. (4分)
因为![]() ,
,![]() ,所以
,所以![]() .
.
故动圆圆心P的轨迹方程是![]() . (6分)
. (6分)
(Ⅱ)因为直线x=5与椭圆无交点,可设直线![]() 的方程为
的方程为![]() .
.
由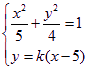 ,得
,得![]() ,即
,即![]() .
.
(8分)
设点![]() ,AB的中点为
,AB的中点为![]() ,则
,则
![]() ,
,![]() . (10分)
. (10分)
若线段AB的垂直平分线经过圆心O2,则CO2⊥![]() ,即
,即![]() .
.
所以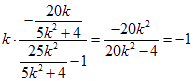 ,即4=0,矛盾! (12分)
,即4=0,矛盾! (12分)
故不存在直线![]() 使得线段AB的垂直平分线经过圆心O2. (13分)
使得线段AB的垂直平分线经过圆心O2. (13分)

练习册系列答案
相关题目
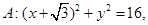 圆心为A;动圆M过点
圆心为A;动圆M过点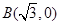 且与圆A相切,圆心M 的坐标为
且与圆A相切,圆心M 的坐标为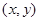 且
且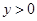 ,它的轨迹记为C。
,它的轨迹记为C。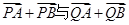 互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。
互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。 ),两个焦点是F1(-1,0)和F2(1,0)
),两个焦点是F1(-1,0)和F2(1,0)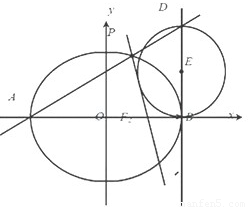
 和Q2:(x-1)2+y2=
和Q2:(x-1)2+y2=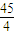 ,动圆P与⊙O1外切,且与⊙O2内切.
,动圆P与⊙O1外切,且与⊙O2内切.