题目内容
已知全集U=R,集合A={x|log2(3-x)≤2},集合B={x| ≥1}.
≥1}.
(1)求A、B;
(2)求(∁UA)∩B.
 ≥1}.
≥1}.(1)求A、B;
(2)求(∁UA)∩B.
解:(1)由已知得log2(3-x)≤log24,
∴ 解得-1≤x<3,
解得-1≤x<3,
∴A={x|-1≤x<3}. 由 ≥1
≥1 ,得(x+2)(x-3)≤0,
,得(x+2)(x-3)≤0,
且x+2≠0,解得-2<x≤3.∴B={x|-2<x≤3}. ------8分
(2)由(1)可得∁UA={x|x<-1或x≥3}.故(∁UA)∩B={x|-2<x<-1或x=3}.
∴
 解得-1≤x<3,
解得-1≤x<3,∴A={x|-1≤x<3}. 由
 ≥1
≥1 ,得(x+2)(x-3)≤0,
,得(x+2)(x-3)≤0,且x+2≠0,解得-2<x≤3.∴B={x|-2<x≤3}. ------8分
(2)由(1)可得∁UA={x|x<-1或x≥3}.故(∁UA)∩B={x|-2<x<-1或x=3}.
略

练习册系列答案
相关题目
 ,
,
 时,求
时,求 ;
;  ,求实数
,求实数 的取值范围.
的取值范围.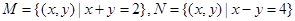 , 那么集合
, 那么集合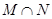 为( )
为( )



 若集合
若集合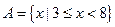 ,
,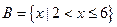 ,则
,则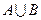 ,
, 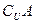 ;
; 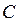 =
=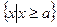 ,
,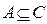 ,求
,求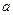 的取值范围;
的取值范围;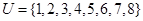 ,集合
,集合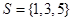 ,
,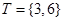 ,则
,则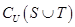 等于( ▲ )
等于( ▲ )
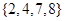
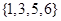
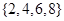
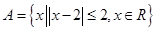 ,
,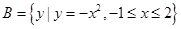 ,则
,则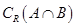 等于
等于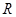 B.
B.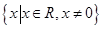 C.
C.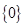 D.
D.