题目内容
在直角坐标平面上有两个区域M和N.M是由y≥0,y≤x和y≥2-x这三个不等式确定的.N是随t变化的区域,它由不等式t≤x≤t+1的确定,t的取值范围是0≤t≤1.设M和N的公共面积是函数f(t),求证:f(t)=-t2+t+![]() .
.
答案:
解析:

解析:
思路与技巧:这是一个基本问题,关键是确定M和N的公共部分的形状.可先画出M、N这两个区域,然后再作判断.
证明:如图所示,依题意,区域M是图中△AOB,区域N是直线x=t与x=t+1(0≤t≤1)之间的带形域.M和N的公共部分为图中的阴影部分五边形ACDEF(包括边界),其面积可由△AOB的面积减去Rt△ODC、Rt△BEF的面积进行计算.


评析:关于五边形ACDEF面积的计算,可从下面三个途径去考虑:
(1)△AOB的面积减去Rt△ODC、Rt△BEF的面积;
(2)过A作x轴的垂线,将其划分为两个直角梯形来计算;
(3)连结CF,将其划分为一个直角三角形CAF和一个直角梯形CDEF去求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
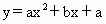 的图像与x轴有两个交点,则点(a,b)在直角坐标平面上表示的区域(不含边界)为
的图像与x轴有两个交点,则点(a,b)在直角坐标平面上表示的区域(不含边界)为

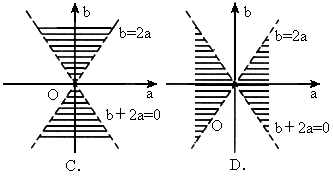
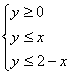 },区域N={(x,y)|t≤x≤t+1,0≤t≤1},区域M和N的公共面积用函数f(t)表示,则f(t)的表达式为( )
},区域N={(x,y)|t≤x≤t+1,0≤t≤1},区域M和N的公共面积用函数f(t)表示,则f(t)的表达式为( )