题目内容
已知函数f(x2-3)=lg
.
(1)求函数f(x)的定义域; (2)判断函数f(x)的奇偶性;
(3)求f(x)的反函数; (4)若f[φ(x)]=lgx,求φ(3)的值.
| x2 | x2-6 |
(1)求函数f(x)的定义域; (2)判断函数f(x)的奇偶性;
(3)求f(x)的反函数; (4)若f[φ(x)]=lgx,求φ(3)的值.
分析:(1)整体代换的思路用换元法求解析式,设x2-3=t,然后利用x2=t+3,代入已知函数,求出f(t),即f(x)的表达式
(2)通过(1)的解析式判断奇偶性,判断定义域是否关于原点对称,然后判断f(-x)与f(x)之间的关系,根据函数奇偶性的定义进行证明.
(3)将f(x)看成关于x的方程,通过解方程求出x,然后将x,y互换得到f(x)的反函数.
(4)把φ(x)代入f(x)的解析式,求出φ(x)的值,把3代入φ(x)即可解出φ(3)的值.
(2)通过(1)的解析式判断奇偶性,判断定义域是否关于原点对称,然后判断f(-x)与f(x)之间的关系,根据函数奇偶性的定义进行证明.
(3)将f(x)看成关于x的方程,通过解方程求出x,然后将x,y互换得到f(x)的反函数.
(4)把φ(x)代入f(x)的解析式,求出φ(x)的值,把3代入φ(x)即可解出φ(3)的值.
解答:解:(1)设x2-3=t(t>-3),
所以原函数转化为f(t)=lg
,
由
>0得定义域为{t|t>3}
即f(x)=lg
,定义域为{x|x>3}
(2)因为f(x)的定义域是(3,+∞)
所以函数f(x)是非奇非偶函数
(3)由f(x)=lg
得
x=
(y∈(0,+∞))
所以f(x)的反函数是f-1(x)=
(x∈(0,+∞))
(4)由f[φ(x)]=lgx可得:f[φ(x)]=lg
=lgx
即:
=x
解得:φ(x)=
则:φ(3)=6
所以原函数转化为f(t)=lg
| t+3 |
| t-3 |
由
| t+3 |
| t-3 |
即f(x)=lg
| x+3 |
| x-3 |
(2)因为f(x)的定义域是(3,+∞)
所以函数f(x)是非奇非偶函数
(3)由f(x)=lg
| x+3 |
| x-3 |
x=
| 3(10y+1) |
| 10y-1 |
所以f(x)的反函数是f-1(x)=
| 3(10x+1) |
| 10x-1 |
(4)由f[φ(x)]=lgx可得:f[φ(x)]=lg
| φ(x)+3 |
| φ(x)-3 |
即:
| φ(x)+3 |
| φ(x)-3 |
解得:φ(x)=
| 3x+3 |
| x-1 |
则:φ(3)=6
点评:本题考查复合函数的定义域及单调性的求解,第三问为创新型题目,为中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
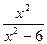 ,
, 定义域;
定义域; ] = lgx,求
] = lgx,求 的值。
的值。